半波整流器

---

半波整流器是一個二極體電路，用於將交流電壓（交流電源）轉換為直流電壓（直流電源）。半波整流器電路中使用單個二極體進行交流電轉換為直流電。

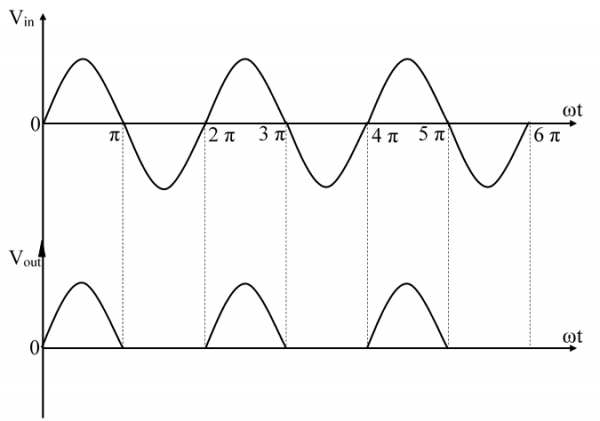
半波整流器電路允許交流電源波形的半個週期透過，並阻擋另一個半個週期。

半波整流器電路圖

HWR 的電路由以下三個主要元件組成：

• 二極體

• 變壓器

• 負載（可能是電阻）

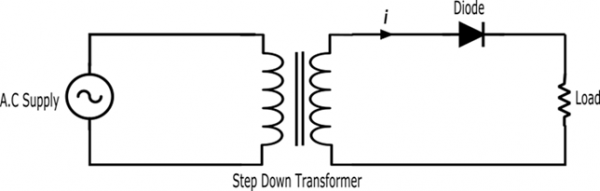
HWR 電路的工作原理

正半週期

交流高電壓施加到降壓變壓器的一次側，獲得的二次低電壓施加到二極體，二極體在正半週期期間處於正向偏置狀態並充當短路。

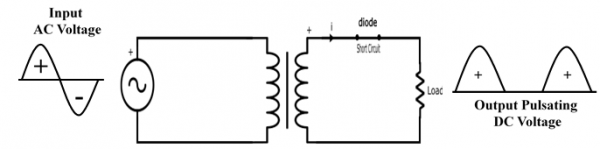
負半週期

在負半週期期間，二極體的 P 端連線到負電源，這會反向偏置二極體，二極體表現為開路，並且不會在負載兩端產生輸出。

半波整流器波形

半波整流器公式

HWR 的效率

HWR 的效率定義為輸出直流功率與輸入交流功率之比。

$$η=\frac{P_{dc}}{P_{ac}}$$

半波整流器的最大效率為 40.6%。

HWR 的峰值反向電壓

HWR 的峰值反向電壓是二極體在施加反向偏置時能夠承受的最大電壓，而不會被破壞。

$\mathrm {PIV} = V_{m}$

HWR 的負載電流的有效值

$$I_{RMS} = \frac{I_{m}}{2}$$

HWR 的負載電流的平均值

$$I_{avg} = \frac{I_{m}}{π}$$

HWR 的波形因子

$$\mathrm{Form\, Factor}=\frac{\mathrm{RMS\, Value}}{\mathrm{Avg.\,Value}}=\frac{V_{\mathrm{rms}}}{V_{\mathrm{avg}}}$$

對於 HWR，波形因子等於 1.57。

HWR 的紋波係數

紋波係數提供有關 HWR 如何將輸入交流電壓轉換為輸出直流電壓的資訊。它由下式給出：

$\mathrm{Ripple\:Factor}=\sqrt{((\mathrm{Form\:Factor})^2 − 1)}$

半波整流器的紋波係數為 1.21。

半波整流器的應用

半波整流器有一些應用：

• 它們用於整流
• 它們用於解調
• 它們用於訊號峰值應用

半波整流器的缺點

• 交流電源僅在半個週期內提供功率。因此，輸出功率較低。
• 負載中的脈動電流包含交流電流，其頻率等於電源頻率。因此，需要濾波以產生穩定的直流電流。

數值示例

一個具有內阻 *R*_*d* = 10Ω 的二極體用於半波整流。如果施加的電壓為 v = 50 sin⁡(ωt) 且負載電阻 *R*_*L* = 10Ω。求以下各項：

• *I*_m、*I*_dc、*I*_rms
• 交流輸入功率和直流輸出功率
• 直流輸出電壓
• 整流效率

解決方案

最大電壓，$V_{m}=50 \, \mathrm{V}$

(a) ${I_{m}=\frac{v_{m}}{R_{d}+R_{L}} = \frac{50}{10+1000}} =0.0495 = 49.5 \thinspace \mathrm {mA}$

${I_{dc}= I_{avg} = \frac{I_{m}}{π}} = \frac{49.5}{π} = 15.76 \thinspace \mathrm {mA}$

${I_{rms} =  \frac{I_{m}}{2}} = \frac{49.5}{2} = 24.75 \thinspace \mathrm {mA}$

(b) $P_{ac}=(I_{\mathrm{rms}})^{2}\: (R_{d}+R_{L})$

$$\Rightarrow P_{ac}=(24.75 \times 10^{-3})^{2} \times  (10 + 1000) = 0.618 \, \mathrm{Watts}$$

     $P_{dc} = (I_{dc})^{2} (R_{L})$

$$\Rightarrow P_{dc} = (15.76 \times 10^{-3})^{2} × (1000) = 0.248 \, \mathrm{Watts}$$

(c) 直流輸出電壓 

$$ = I_{dc} \times R_{L}$$

$$ = (15.76 \times 10^{-3}) \times 1000 = 15.76 \, \mathrm{V}$$

(d) $\mathrm{Efficiency}(\eta)= \frac{P_{dc}}{P_{ac}} = \frac{0.248}{0.618} \times 100 = 40.12%$