資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究全波整流器
全波整流器是一種二極體電路，用於將交流電壓（交流電源）的完整週期轉換為直流電壓（直流電源）。
在全波整流中，電流在交流電源的整個週期內都沿相同方向流過負載。
全波整流器的型別
- 中心抽頭全波整流器
- 橋式全波整流器
中心抽頭全波整流器
中心抽頭全波整流器的電路包含以下主要元件：
- 兩個二極體
- 一箇中心抽頭變壓器
- 一個負載電阻
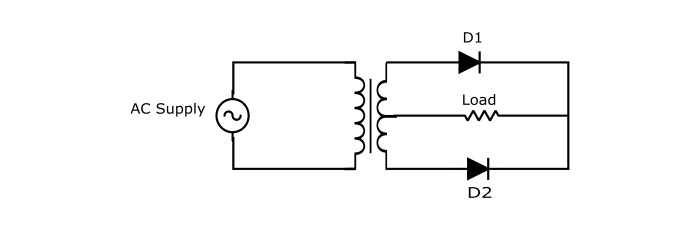
中心抽頭全波整流器電路的工作原理
正半週期
在輸入交流電壓的正半週期內，次級繞組的A端為正，B端為負。這使得二極體D1正向偏置（像閉合開關一樣），二極體D2反向偏置（像斷開開關一樣）。因此，電流從P點流經負載（RL）到O點。
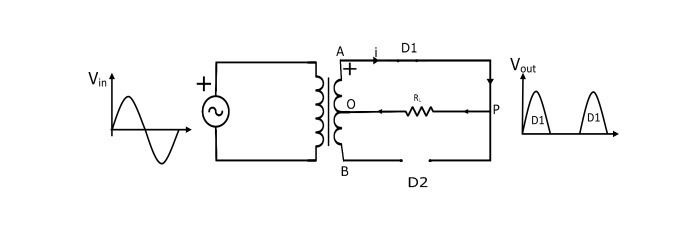
負半週期
在輸入交流電源的負半週期內，次級繞組的B端為正，A端為負。這使得二極體D2正向偏置（像閉合開關一樣），二極體D1反向偏置（像斷開開關一樣）。因此，電流將從B點流經二極體D2、負載RL和次級繞組的下半部分到O點。
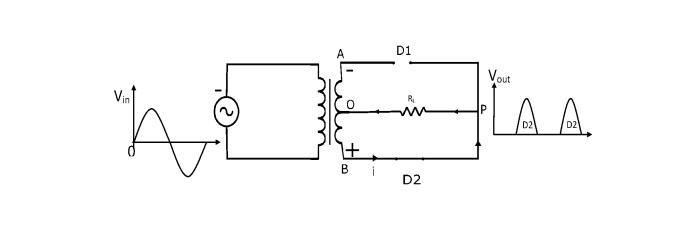
請注意，負載電流在輸入交流電源的兩個半週期內方向相同。因此，在負載上獲得直流輸出。
中心抽頭全波整流器的輸出頻率
輸出頻率是輸入頻率的兩倍。由於輸入電源是每2π弧度重複一次的正弦波。全波整流器的輸出是脈動的直流電，每2π弧度內重複輸入交流電的相同模式兩次。
$$\mathrm{f_{out}=2f_{in}}$$
中心抽頭全波整流器的缺點
- 二極體必須具有峰值反向電壓。
- 很難在次級繞組上找到中心抽頭。
橋式全波整流器
橋式全波整流器消除了對中心抽頭變壓器的需求。它包含四個連線成橋的二極體。
橋式全波整流器的電路圖
橋式全波整流器的電路包含以下主要元件：
- 四個二極體
- 一個降壓變壓器
- 一個負載電阻
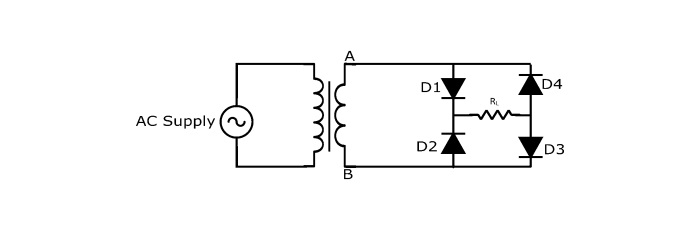
橋式全波整流器的電路工作原理
正半週期
在正半週期內，次級繞組的A端為正，B端為負。這使得二極體D1和D3正向偏置（像閉合開關一樣），二極體D2和D4反向偏置（像斷開開關一樣）。電流從A點流經二極體D1、負載RL和二極體D3到B點。
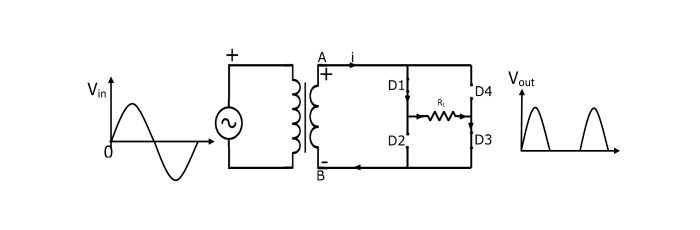
負半週期
在負半週期內，次級繞組的A端為負，B端為正。這使得二極體D1和D3反向偏置（像斷開開關一樣），二極體D2和D4正向偏置（像閉合開關一樣）。電流從B點流經二極體D2、負載RL和二極體D4到A點。
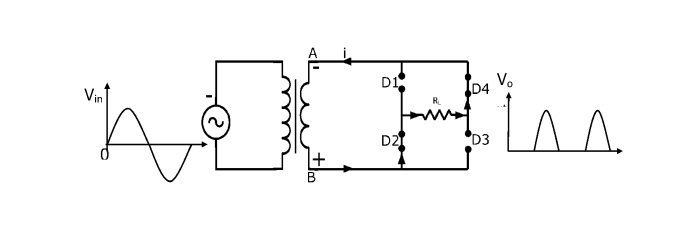
因此，電流在輸入交流電源的兩個週期內都沿相同方向流過負載RL。因此，在負載上獲得直流輸出。
橋式全波整流器的優點
對於相同的次級電壓，輸出是中心抽頭全波整流器的兩倍。
不需要中心抽頭變壓器。
對於相同的直流輸出，橋式全波整流器的PIV是中心抽頭全波整流器的一半。
橋式全波整流器的缺點
它需要四個二極體。
在交流輸入的每個半週期內，導通的兩個二極體串聯，這會導致二極體內阻壓降。
全波整流器波形
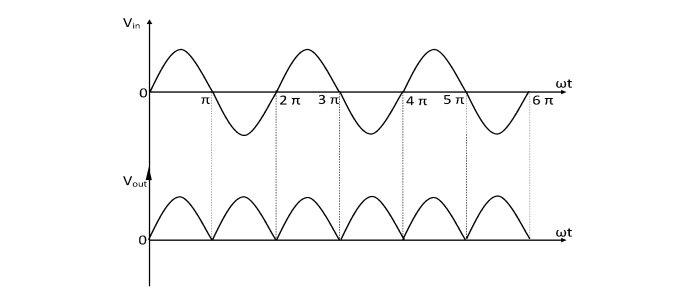
全波整流器公式
全波整流器的效率
全波整流器的效率定義為直流輸出功率與交流輸入功率之比。
$$\mathrm{\eta=\frac{P_{dc}}{P_{ac}}}$$
全波整流器的最大效率為81.2%。
全波整流器的峰值反向電壓
“PIV是二極體在反向偏置時可以承受的最大電壓，超過此電壓將導致二極體損壞。”
對於中心抽頭全波整流器，PIV是最大次級繞組電壓的兩倍。
$$\mathrm{PIV=2V_{m}}$$
對於橋式全波整流器，每個二極體的PIV等於最大次級電壓。
$$\mathrm{PIV=V_{m}}$$
全波整流器負載電流的有效值
$$\mathrm{I_{RMS}=\frac{I_{m}}{\sqrt{2}}}$$
全波整流器負載電流的平均值
$$\mathrm{I_{RMS}=\frac{2I_{m}}{\pi}}$$
全波整流器的直流輸出電壓
$$\mathrm{V_{dc}=V_{dc}R_{L}=V_{avg}R_{L}}$$
全波整流器的波形係數
$$\mathrm {{波形係數}=\frac{有效值}{平均值}=\frac{V_{rms}}{V_{avg}}}$$
對於全波整流器，波形係數等於1.11。
全波整流器的紋波係數
紋波係數提供了關於全波整流器如何將交流輸入電壓轉換為直流輸出電壓的資訊。它由下式給出：
$$\mathrm{紋波係數=\sqrt{(波形係數)^2}-1}$$
全波整流器的紋波係數為0.482。
數值例題 #1
在一箇中心抽頭全波整流器中，每個二極體的內阻為。從中心抽頭到次級繞組每一端的變壓器次級有效電壓為60 V，負載電阻為。求：
- 平均負載電流
- 負載電流的有效值
- 直流輸出電壓
- 峰值反向電壓
解答
次級繞組半邊的有效電壓，Vrms=60V
次級繞組半邊的最大電壓，$V_{m}=60×\sqrt{2}=84.84 V$
$$\mathrm{(∵ V_{m}=V_{rms}×√2 )}$$
$$\mathrm{I_{m}=\frac{V_{m}}{R_{d}+R_{L}}=\frac{84.84}{(10+870)}=96.41 mA}$$
(a) 平均負載電流
$$\mathrm{I_{avg}=\frac{2I_{m}}{\pi}=\frac{2×96.41}{\pi}=61.41 mA}$$
(b) 負載電流的有效值
$$\mathrm{I_{rms}=\frac{I_{m}}{\sqrt{2}}=\frac{96.41}{\sqrt{2}}=68.18 mA}$$
(c) 直流輸出電壓
$$\mathrm{V_{dc}=I_{avg}R_{L}=61.41×870=53.43 V}$$
(d) 峰值反向電壓
$$\mathrm{PIV=2V_{m}=2×84.84=169.68 V}$$
數值例題 #2
在一個橋式全波整流器電路中，每個二極體的正向電阻為2Ω，反向電阻為無窮大。交流電源電壓為230 V有效值，負載電阻為50Ω。計算：
- (a) 平均負載電流
- (b) 整流器效率
解答
電源電壓的有效值
$$\mathrm{V_{rms}=230 V}$$
電源電壓的最大值
$$\mathrm{V_{m}=230×√2=325.22 V}$$
負載電流的最大值
$$\mathrm{I_{m}=\frac{V}{2R_{d}+R_{L}}=\frac{325.22}{(4+50)}=6.02 A}$$
(a) 平均負載電流
$$\mathrm{I_{avg}=\frac{2I_{m}}{\pi}=\frac{2×6.02}{\pi}=3.83 A}$$
(b) 負載電流的有效值
$$\mathrm{I_{rms}=\frac{I_{m}}{\sqrt{2}}=\frac{6.02}{\sqrt{2}}=4.26 A}$$
整流器效率，
$$ \mathrm{\eta=\frac{P_{dc}}{P_{ac}}=\frac{I_{avg}^2×R_{L}}{(I_{rms})^2×(2R_{d}+R_{L})}=\frac{3.83^2×50}{4.26^2×54}×100=74.84\%}$$
27K+ 瀏覽量
