Python探索性資料分析

對於資料分析，探索性資料分析 (EDA) 必須是你的第一步。探索性資料分析幫助我們：

  • 深入瞭解資料集。

  • 理解底層結構。

  • 提取重要的引數及其之間的關係。

  • 檢驗底層假設。

使用示例資料集理解EDA

為了使用Python理解EDA，我們可以直接從任何網站或本地磁盤獲取示例資料。我從公開可用的UCI機器學習資源庫中獲取了紅葡萄酒質量資料集的樣本資料，並嘗試使用EDA深入瞭解該資料集。

import pandas as pd
df = pd.read_csv("http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv")
df.head()

在Jupyter Notebook中執行上述指令碼，將得到如下輸出：

首先：

  • 首先，匯入必要的庫，在本例中是pandas。

  • 使用pandas庫的read_csv()函式讀取csv檔案，給定資料集中每個資料用分號“;”分隔。

  • 使用pandas庫提供的“.head”函式返回資料集的前五個觀測值。我們可以透過使用pandas庫的“.tail()”函式類似地獲取最後五個觀測值。

我們可以使用“.shape”獲取資料集的行數和列數，如下所示：

df.shape

藉助info()函式，我們可以找到它包含的所有列、列的型別以及它們是否包含任何值。

df.info()

透過觀察上述資料，我們可以得出結論：

  • 資料只包含浮點型和整型值。

  • 所有列變數均非空（無空值或缺失值）。

pandas提供的另一個有用的函式是describe()，它提供了資料的計數、均值、標準差、最小值和最大值以及數量。

df.describe()

  • 從上述資料中，我們可以得出結論，每列的均值都小於索引列中的中位數（50%）。

  • 預測變數“殘糖”、“遊離二氧化硫”和“總二氧化硫”的75%值和最大值之間存在巨大差異。

  • 上述兩個觀察結果表明，我們的資料集中存在極值偏差。

我們可以從因變數中獲得一些關鍵見解，如下所示：

df.quality.unique()

  • 在“質量”評分量表中，1位於底部，即差；10位於頂部，即好。

  • 從上面我們可以得出結論，沒有觀測值得分1（差）、2和9、10（好）。所有分數都在3到8之間。

df.quality.value_counts()

  • 上述處理後的資料提供了每個質量得分按降序排列的投票數資訊。

  • 大部分質量都在5-7的範圍內。

  • 在3和6類別中觀察到的觀測值最少。

資料視覺化

檢查缺失值：

我們可以藉助seaborn庫檢查我們的白威士忌csv資料集中的缺失值。以下是實現此目的的程式碼：

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
sns.set()
df = pd.read_csv("http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-white.csv", sep=";")
sns.heatmap(df.isnull(), cbar=False, yticklabels=False, cmap='viridis')

輸出

  • 從上面我們可以看到，資料集中沒有缺失值。如果有任何缺失值，我們將在紫色背景上看到用不同顏色陰影表示的圖形。

  • 對於存在缺失值的不同資料集，你會注意到差異。

檢查相關性

要檢查資料集不同值之間的相關性，請在現有資料集中插入以下程式碼：

plt.figure(figsize=(8,4))
sns.heatmap(df.corr(),cmap='Greens',annot=False)

輸出

  • 上面，正相關用深色陰影表示，負相關用淺色陰影表示。

  • 將annot=True的值更改，輸出將顯示特徵在網格單元中相互關聯的值。

我們可以使用annot=True生成另一個相關矩陣。透過在現有程式碼中新增以下程式碼行來修改你的程式碼：

k = 12
cols = df.corr().nlargest(k, 'quality')['quality'].index
cm = df[cols].corr()
plt.figure(figsize=(8,6))
sns.heatmap(cm, annot=True, cmap = 'viridis')

輸出

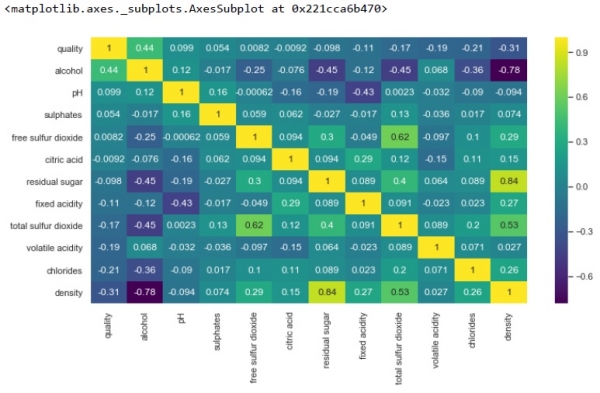
  • 從上面我們可以看到，密度與殘糖之間存在很強的正相關性。然而，密度與酒精之間存在很強的負相關性。

  • 此外，遊離二氧化硫與質量之間沒有相關性。

更新於：2019年7月30日

2K+ 瀏覽量

啟動你的職業生涯

透過完成課程獲得認證

開始
廣告