
- 分散式資料庫管理系統教程
- DDBMS - 首頁
- DDBMS - 資料庫管理系統概念
- DDBMS - 分散式資料庫
- 分散式資料庫設計
- 分散式資料庫環境
- DDBMS - 設計策略
- DDBMS - 分散式透明性
- DDBMS - 資料庫控制
- 分散式資料庫管理系統安全性
- 資料庫安全與加密
- 分散式資料庫中的安全性
- 分散式資料庫管理系統資源
- DDBMS - 快速指南
- DDBMS - 有用資源
- DDBMS - 討論
關係代數在查詢最佳化中的應用
當提交一個查詢時,首先會掃描、解析和驗證它。然後建立一個查詢的內部表示,例如查詢樹或查詢圖。接下來,會設計出從資料庫表中檢索結果的備選執行策略。選擇最合適的查詢處理執行策略的過程稱為查詢最佳化。
DDBMS 中的查詢最佳化問題
在 DDBMS 中,查詢最佳化是一項至關重要的任務。由於以下因素,其複雜性很高,因為備選策略的數量可能會呈指數級增長:
- 存在多個碎片。
- 碎片或表分佈在不同的站點。
- 通訊鏈路的速率。
- 本地處理能力的差異。
因此,在分散式系統中,目標通常是找到一個好的查詢處理執行策略,而不是最好的策略。執行查詢的時間是以下時間的總和:
- 將查詢傳送到資料庫的時間。
- 執行本地查詢片段的時間。
- 從不同站點彙集資料的時間。
- 將結果顯示給應用程式的時間。
查詢處理
查詢處理是一組從查詢放置到顯示查詢結果的所有活動。步驟如下面的圖所示:
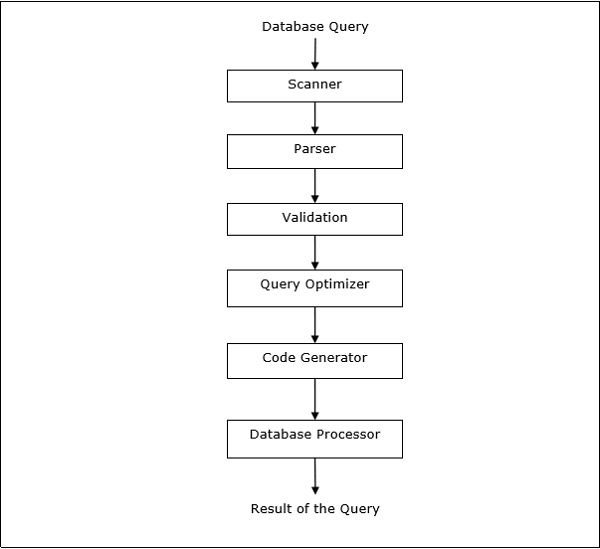
關係代數
關係代數定義了關係資料庫模型的基本操作集。一系列關係代數操作構成一個關係代數表示式。該表示式的結果表示資料庫查詢的結果。
基本操作包括:
- 投影
- 選擇
- 並集
- 交集
- 差集
- 連線
投影
投影操作顯示錶中欄位的子集。這會對錶進行垂直分割。
關係代數語法
$$\pi_{<{AttributeList}>}{(<{Table Name}>)}$$
例如,讓我們考慮以下學生資料庫:
| 學號 | 姓名 | 課程 | 學期 | 性別 |
| 2 | Amit Prasad | BCA | 1 | 男 |
| 4 | Varsha Tiwari | BCA | 1 | 女 |
| 5 | Asif Ali | MCA | 2 | 男 |
| 6 | Joe Wallace | MCA | 1 | 男 |
| 8 | Shivani Iyengar | BCA | 1 | 女 |
如果我們想顯示所有學生的姓名和課程,我們將使用以下關係代數表示式:
$$\pi_{Name,Course}{(STUDENT)}$$
選擇
選擇操作顯示滿足某些條件的表中元組的子集。這會對錶進行水平分割。
關係代數語法
$$\sigma_{<{Conditions}>}{(<{Table Name}>)}$$
例如,在 Student 表中,如果我們想顯示所有選擇了 MCA 課程的學生的詳細資訊,我們將使用以下關係代數表示式:
$$\sigma_{Course} = {\small "BCA"}^{(STUDENT)}$$
投影和選擇操作的組合
對於大多數查詢,我們需要組合投影和選擇操作。有兩種方法可以編寫這些表示式:
- 使用投影和選擇操作的序列。
- 使用重新命名操作生成中間結果。
例如,要顯示所有 BCA 課程的女學生的姓名:
- 使用投影和選擇操作序列的關係代數表示式
$$\pi_{Name}(\sigma_{Gender = \small "Female" AND \: Course = \small "BCA"}{(STUDENT)})$$
- 使用重新命名操作生成中間結果的關係代數表示式
$$FemaleBCAStudent \leftarrow \sigma_{Gender = \small "Female" AND \: Course = \small "BCA"} {(STUDENT)}$$
$$Result \leftarrow \pi_{Name}{(FemaleBCAStudent)}$$
並集
如果 P 是一個操作的結果,Q 是另一個操作的結果,則 P 和 Q 的並集($p \cup Q$)是 P 中、Q 中或兩者中所有元組的集合,但不包含重複項。
例如,要顯示所有在第 1 學期或選擇了 BCA 課程的學生:
$$Sem1Student \leftarrow \sigma_{Semester = 1}{(STUDENT)}$$
$$BCAStudent \leftarrow \sigma_{Course = \small "BCA"}{(STUDENT)}$$
$$Result \leftarrow Sem1Student \cup BCAStudent$$
交集
如果 P 是一個操作的結果,Q 是另一個操作的結果,則 P 和 Q 的交集($p \cap Q$)是 P 和 Q 中都存在的元組的集合。
例如,給出以下兩個模式:
EMPLOYEE
| EmpID | 姓名 | 城市 | 部門 | 薪資 |
PROJECT
| PId | 城市 | 部門 | 狀態 |
要顯示所有專案所在地和員工居住地的城市名稱:
$$CityEmp \leftarrow \pi_{City}{(EMPLOYEE)}$$
$$CityProject \leftarrow \pi_{City}{(PROJECT)}$$
$$Result \leftarrow CityEmp \cap CityProject$$
差集
如果 P 是一個操作的結果,Q 是另一個操作的結果,則 P - Q 是 P 中但不在 Q 中的所有元組的集合。
例如,列出所有沒有正在進行的專案的部門(狀態為“正在進行”的專案):
$$AllDept \leftarrow \pi_{Department}{(EMPLOYEE)}$$
$$ProjectDept \leftarrow \pi_{Department} (\sigma_{Status = \small "ongoing"}{(PROJECT)})$$
$$Result \leftarrow AllDept - ProjectDept$$
連線
連線操作將兩個不同表(查詢的結果)中相關的元組組合到一個表中。
例如,考慮銀行資料庫中的兩個模式 Customer 和 Branch,如下所示:
CUSTOMER
| CustID | AccNo | TypeOfAc | BranchID | DateOfOpening |
BRANCH
| BranchID | BranchName | IFSCcode | Address |
要列出員工詳細資訊以及分支詳細資訊:
$$Result \leftarrow CUSTOMER \bowtie_{Customer.BranchID=Branch.BranchID}{BRANCH}$$
將 SQL 查詢轉換為關係代數
在最佳化之前,SQL 查詢會被轉換為等效的關係代數表示式。查詢首先被分解成更小的查詢塊。這些塊被轉換為等效的關係代數表示式。最佳化包括最佳化每個塊,然後最佳化整個查詢。
示例
讓我們考慮以下模式:
EMPLOYEE
| EmpID | 姓名 | 城市 | 部門 | 薪資 |
PROJECT
| PId | 城市 | 部門 | 狀態 |
WORKS
| EmpID | PID | Hours |
示例 1
要顯示所有薪資低於平均薪資的員工的詳細資訊,我們編寫 SQL 查詢:
SELECT * FROM EMPLOYEE WHERE SALARY < ( SELECT AVERAGE(SALARY) FROM EMPLOYEE ) ;
此查詢包含一個巢狀子查詢。因此,可以將其分解成兩個塊。
內部塊是:
SELECT AVERAGE(SALARY)FROM EMPLOYEE ;
如果此查詢的結果為 AvgSal,則外部塊為:
SELECT * FROM EMPLOYEE WHERE SALARY < AvgSal;
內部塊的關係代數表示式:
$$AvgSal \leftarrow \Im_{AVERAGE(Salary)}{EMPLOYEE}$$
外部塊的關係代數表示式:
$$\sigma_{Salary <{AvgSal}>}{EMPLOYEE}$$
示例 2
要顯示員工“Arun Kumar”的所有專案的專案 ID 和狀態,我們編寫 SQL 查詢:
SELECT PID, STATUS FROM PROJECT
WHERE PID = ( SELECT FROM WORKS WHERE EMPID = ( SELECT EMPID FROM EMPLOYEE
WHERE NAME = 'ARUN KUMAR'));
此查詢包含兩個巢狀子查詢。因此,可以將其分解成三個塊,如下所示:
SELECT EMPID FROM EMPLOYEE WHERE NAME = 'ARUN KUMAR'; SELECT PID FROM WORKS WHERE EMPID = ArunEmpID; SELECT PID, STATUS FROM PROJECT WHERE PID = ArunPID;
(此處 ArunEmpID 和 ArunPID 是內部查詢的結果)
三個塊的關係代數表示式:
$$ArunEmpID \leftarrow \pi_{EmpID}(\sigma_{Name = \small "Arun Kumar"} {(EMPLOYEE)})$$
$$ArunPID \leftarrow \pi_{PID}(\sigma_{EmpID = \small "ArunEmpID"} {(WORKS)})$$
$$Result \leftarrow \pi_{PID, Status}(\sigma_{PID = \small "ArunPID"} {(PROJECT)})$$
關係代數運算子的計算
關係代數運算子的計算可以透過多種不同的方式完成,每種備選方案稱為**訪問路徑**。
計算備選方案取決於三個主要因素:
- 運算子型別
- 可用記憶體
- 磁碟結構
執行關係代數運算的時間是以下時間的總和:
- 處理元組的時間。
- 從磁碟將表的元組提取到記憶體的時間。
由於處理元組的時間遠小於從儲存中提取元組的時間,尤其是在分散式系統中,因此磁碟訪問通常被視為計算關係表示式成本的指標。
選擇的計算
選擇操作的計算取決於選擇條件的複雜性和表屬性上索引的可用性。
以下是根據索引的不同計算備選方案:
**無索引** - 如果表未排序且沒有索引,則選擇過程涉及掃描表的全部磁碟塊。每個塊都被載入到記憶體中,並檢查塊中的每個元組以檢視它是否滿足選擇條件。如果滿足條件,則將其顯示為輸出。這是成本最高的方案,因為每個元組都被載入到記憶體中,並且每個元組都被處理。
**B+ 樹索引** - 大多數資料庫系統都建立在 B+ 樹索引之上。如果選擇條件基於此 B+ 樹索引的鍵欄位,則使用此索引檢索結果。但是,處理具有複雜條件的選擇語句可能涉及大量磁碟塊訪問,在某些情況下甚至需要完全掃描表。
**雜湊索引** - 如果使用雜湊索引並且其鍵欄位用於選擇條件,則使用雜湊索引檢索元組將變得非常簡單。雜湊索引使用雜湊函式查詢儲存與雜湊值對應的鍵值的桶的地址。為了在索引中查詢鍵值,執行雜湊函式並找到桶地址。搜尋桶中的鍵值。如果找到匹配項,則從磁碟塊將實際元組提取到記憶體中。
連線的計算
當我們想要連線兩個表(例如 P 和 Q)時,必須將 P 中的每個元組與 Q 中的每個元組進行比較,以測試是否滿足連線條件。如果滿足條件,則連線相應的元組,消除重複欄位並將其附加到結果關係。因此,這是最昂貴的操作。
計算連線的常用方法包括:
巢狀迴圈方法
這是傳統的連線方法。可以透過以下虛擬碼進行說明(表 P 和 Q,元組 tuple_p 和 tuple_q,連線屬性 a):
For each tuple_p in P For each tuple_q in Q If tuple_p.a = tuple_q.a Then Concatenate tuple_p and tuple_q and append to Result End If Next tuple_q Next tuple-p
排序合併方法
在這種方法中,兩個表根據連線屬性分別進行排序,然後將排序後的表合併。由於記錄數量非常多,無法容納在記憶體中,因此採用了外部排序技術。一旦各個表排序完成,將每個排序表中的一頁載入到記憶體中,根據連線屬性進行合併,並將連線後的元組寫入輸出。
雜湊連線方法
此方法包括兩個階段:分割槽階段和探測階段。在分割槽階段,表 P 和 Q 被分成兩組不相交的分割槽。確定一個共同的雜湊函式。此雜湊函式用於將元組分配到分割槽。在探測階段,將 P 的一個分割槽中的元組與 Q 的對應分割槽的元組進行比較。如果匹配,則將其寫入輸出。