頂點間距離和偏心率

兩個頂點之間的距離

它是頂點U和頂點V之間最短路徑中的邊數。如果有多條路徑連線兩個頂點，則最短路徑被認為是這兩個頂點之間的距離。

符號 − d(U,V)

從一個頂點到另一個頂點可能存在任意數量的路徑。在這些路徑中，您只需要選擇最短的一條。

示例

看一下下面的圖：

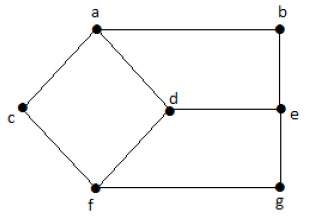
這裡，從頂點“d”到頂點“e”的距離，或簡稱為“de”，是1，因為它們之間有一條邊。從頂點“d”到頂點“e”有很多路徑：

• da, ab, be
• df, fg, ge
• de（它被認為是頂點之間的距離）
• df, fc, ca, ab, be
• da, ac, cf, fg, ge

頂點的偏心率

從一個頂點到所有其他頂點的最大距離被認為是該頂點的偏心率。

符號 − e(V)

獲取從特定頂點到圖中所有其他頂點的距離，在這些距離中，偏心率是距離中最大的一個。

示例

在上圖中，“a”的偏心率是3。

從“a”到“b”的距離是1（'ab'），

從“a”到“c”的距離是1（'ac'），

從“a”到“d”的距離是1（'ad'），

從“a”到“e”的距離是2（'ab'-'be'）或（'ad'-'de'），

從“a”到“f”的距離是2（'ac'-'cf'）或（'ad'-'df'），

從“a”到“g”的距離是3（'ac'-'cf'-'fg'）或（'ad'-'df'-'fg'）。

因此，偏心率是3，這是從頂點“a”到距離最大的“ag”之間的最大距離。

換句話說，

e(b) = 3

e(c) = 3

e(d) = 2

e(e) = 3

e(f) = 3

e(g) = 3

連通圖的半徑

所有頂點中最小偏心率被認為是圖G的半徑。所有頂點到所有其他頂點之間最大距離中的最小值被認為是圖G的半徑。

符號 − r(G)

在圖中所有頂點的偏心率中，連通圖的半徑是所有這些偏心率中的最小值。

示例 −在上圖中，r(G) = 2，這是“d”的最小偏心率。

圖的直徑

所有頂點中最大偏心率被認為是圖G的直徑。所有頂點到所有其他頂點之間最大距離中的最大值被認為是圖G的直徑。

符號 − d(G)

在圖中所有頂點的偏心率中，連通圖的直徑是所有這些偏心率中的最大值。

示例 −在上圖中，d(G) = 3；這是最大偏心率。

Mahesh Parahar

更新於：2019年8月23日

4K+ 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習