立方體和長方體的區別

---

介紹

立方體和長方體的區別在於，立方體有六個大小相同的正方形面，而長方體有矩形面。只有長方體和立方體是兩種具有某些共同特徵的立體圖形，例如它們都有六個面、八個頂點和十二條邊。幾何學中還有許多形狀，例如圓柱體、球體和圓錐體，它們具有不同的特性。此外，所有內角均為90度。

在本教程中，我們將討論立方體和長方體的區別。

多面體

多面體是具有直邊、平面、直邊和銳頂點（角）的3D形狀。“多面體”一詞源於希臘語“poly”，意思是“許多”，而“polyhedron”則表示“區域或表面”。因此，當許多平面連線在一起時，它們就形成了一個多面體。這些形狀根據它們的通常是多邊形的表面命名。

根據它們的邊，多面體可分為兩種型別。它們是正多面體和不正多面體。

正多面體

如果正多面體的面是全等且規則的多邊形，則它也被稱為柏拉圖立體。正多面體的所有多面角都相等。存在五種正多面體。

不正多面體

不正多面體是指具有不彼此全等的不規則多邊形面以及不等的多面角的多面體。

• 尤拉公式可以表示為

$$\mathrm{F\:+\:V\:-\:E\:=\:2}$$

其中 F 表示面的數量，V 表示頂點的數量，E 表示邊的數量。

立方體

• 立方體是由大小相同的正方形面組成的三維圖形。立方體的所有角都相交於900。立方體的六個相等的面都是正方形。它包含12條相同的邊和8個頂點。

• 下面所示的立方體的尺寸為 l（長度）、b（寬度）和 h（高度）。立方體的邊由它的長度、寬度和高度表示。三條邊相交的點稱為頂點。

長方體

• 具有矩形面的三維圖形稱為長方體。長方體是一個具有盒狀形狀的圖形。此外，長方體有8個頂點和12條邊。長方體的面和邊並不都相等。另一方面，長方體的相對面是相等的。

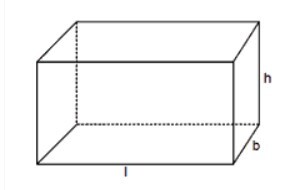
• 長方體如下圖所示，其中 l 等於長度，b 等於寬度，h 等於高度，$\mathrm{l\neq\:b\neq\:h}$。

立方體和長方體的區別

立方體	長方體
高度、寬度和長度的大小都相同。側面和邊相等。	高度、寬度和距離測量值不相等。即，側面和邊不相等。
立方體的六個面都是正方形。	長方體的六個面都是矩形。
立方體的表面積測量值為1，共有12條對角線。	長方體共有12條對角線，其中3條在測量上是不同的。
示例包括魔方、骰子和冰塊。	長方體的示例包括午餐盒和磚塊。
立方體是正方形的三維對應物。	三維中的矩形稱為長方體。
立方體的四個內部對角線的大小都應該相同。	長方體有四個內部對角線，兩對內部角的測量值不同。
總表面積 $\mathrm{=\:6a^{2}}$	總表面積 $\mathrm{=\:2(lb\:+\:bh\:+\:hl)}$
曲面面積 $\mathrm{=\:4a^{2}}$	曲面面積 $\mathrm{=\:2h\:(l\:+\:b)}$
$\mathrm{體積\:=\:a^{3}}$	$\mathrm{體積\:=\:l\times\:b\times\:h}$

例題

1) 求邊長為2的立方體的體積。

答案 - 我們知道立方體體積的公式是 $\mathrm{a^{3}}$

$$\mathrm{立方體體積\:=\:a^{3}}$$

$$\mathrm{=\:2^{3}\:=\:8}$$

2) 求長、寬、高分別為2、3和4的長方體的體積。

答案 - 我們知道長方體體積的公式是 $\mathrm{l\times\:b\times\:h}$

$$\mathrm{立方體體積\:=\:l\times\:b\times\:h}$$

$$\mathrm{=\:2\times\:3\times\:4}$$

$$\mathrm{=\:24}$$

3) 如果立方體的邊長為4，則立方體的表面積是多少？

答案 - 給定立方體的邊長為4，我們知道立方體表面積的公式是 $\mathrm{6a^{2}}$

$$\mathrm{立方體表面積\:=\:6a^{2}}$$

$$\mathrm{=\:6.4^{2}\:=\:96}$$

4) 立方體有多少個頂點（角）？

答案 - 八個。

5) 多面體能否有11個面、22個頂點和33條邊？

答案 - 這可以透過尤拉公式輕鬆驗證。

$$\mathrm{F\:+\:V\:-\:E\:=\:2}$$

給定，面(F) = 11

頂點 (V) = 22

邊(E) = 33

現在將這些代入上述公式，

$$\mathrm{LHS\:=\:F\:+\:V\:-\:E}$$

$$\mathrm{=\:11\:+\:22\:-\:33\:=\:0}$$

$$\mathrm{RHS\:=\:2}$$

$\mathrm{\Longrightarrow}$ LHS 不等於 RHS

因此，對於給定條件，不存在這樣的多面體。

6) 一個立體圖形有14個面和12個頂點。該立體圖形有多少條邊？

答案 - 多面體公式/尤拉公式 $\mathrm{f\:-\:V\:-\:E\:=\:2}$

因此，$\mathrm{14\:+\:12\:-\:E\:=\:2}$

或，$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:26\:-\:E\:=\:2}$

或，$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:E\:=\:26\:-\:2\:=\:24}$

或，$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:E\:=\:24}$

因此，該立體圖形有24條邊

結論

立方體和長方體之間的主要區別在於，立方體有六個大小相同的正方形面，而長方體有矩形面。儘管立方體和長方體的結構相似，但根據它們的邊長、對角線和麵的長度，它們在某些方面有所不同。

常見問題

1. 立方體和長方體具體有什麼不同？

儘管立方體和長方體的結構相當相似，但每種形狀在邊、長度、對角線和麵的方面都存在差異。立方體有六個大小相同的正方形面，而長方體有矩形面。立方體是正方形的，而長方體是矩形的。

2. 長方體能否也稱為立方體？

由於立方體是一個3D正方形物體，其所有側面的長度、寬度和高度都相等，因此它可以被稱為特殊的長方體。立方體由六個面、十二條邊和八個頂點組成，每個頂點連線三個面和三條邊。立方體的相對邊彼此相等且平行。另一方面，長方體是一個3D矩形形狀，其側面不相等。

3. 長方體是什麼形狀？

長方體是一個3D圖形，具有盒狀形狀，並有三對相對的矩形面。長方體由六個面組成，每對相對面都等於另一對。

4. 我們能把立方體稱為正方形嗎？

不能，正方形不能被稱為立方體，因為它們的大小不同。立方體是一個3D圖形，具有長度、寬度和高度，而正方形是一個2D圖形，具有長度和寬度。立方體有12條邊和8個頂點，而正方形有4條邊和4個頂點。