長方體

---

簡介

在幾何學中，長方體是一種立體圖形或三維圖形。長方體是一種具有 8 個頂點、12 條邊和 6 個矩形面的凸多面體。長方體也稱為矩形稜柱。現實世界中長方體的例子是矩形盒子。

什麼是長方體？

想象一下，將許多全等的矩形一個疊一個地堆疊起來形成的形狀。所得的形狀稱為長方體。

長方體的尺寸

為了描述長方體形狀的邊長、寬（或稱深度）或高，需要強調的是，沒有通用的公式。假設長方體的水平面有兩個維度：長和寬，其中長是兩者中較大的一個。當長方體平放在桌子上時，其高度被認為對應於任何垂直邊的長度。字母“l”、“w”和“h”分別代表長方體的長、寬（或稱深度）和高。長方體的邊是連線兩個相鄰頂點的線段的一部分，其頂點是兩條或多條邊相交的位置，其面是其平坦的表面。

長方體的面、邊和頂點

每個 3D 形狀都有固定數量的面、邊和頂點。長方體有六個面、十二條邊和八個頂點。除了 4 個側面外，長方體還有 2 個頂面和底面。它們都是矩形。它有 12 條邊，包括 4 條連線邊和頂面和底面的 8 條邊。其另外 8 個頂點由頂面和底面的頂點組成。在每個頂點處，來自三個維度中的每一個的三個線段匯合在一起。

長方體的公式

請參考下表以瞭解基本的長方體公式。長方體有三個主要維度：l、w 和 h。

面對角線	$\mathrm{\sqrt{(l^{2}\:+\:w^{2})}\:單位}$
空間對角線	$\mathrm{\sqrt{(l^{2}\:+\:w^{2}\:+\:h^{2})}\:單位}$
周長	$\mathrm{4(l\:+\:w\:+\:h)\:單位}$

長方體的對角線

由於長方體是三維形狀，因此它有兩種不同型別的對角線 -

• 面對角線

• 空間對角線

請檢視下圖，該圖描繪了長方體的面和空間對角線。

面對角線

可以透過連線某個長方體面的相對頂點來形成面對角線，但在單個長方體面上只能形成兩條對角線。由於長方體有 6 個面，因此可以畫出總共 12 條面對角線。

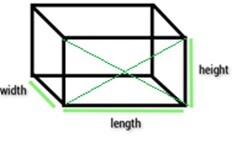
空間對角線

連線長方體相對頂點的線段稱為空間對角線。空間對角線穿過長方體的內部。因此，可以在其內部繪製 4 條空間對角線。

長方體的表面積

長方體的表面積是該形狀佔據的總面積。由於長方體是三維物體，因此其表面積將取決於其長、寬和高。它可能具有的兩種不同型別的表面積是總表面積和側表面積。因此，提供以下公式來確定長方體的表面積

長方體的總表面積等於 $\mathrm{S\:=\:2\:(lb\:+\:bh\:+\:lh)\:平方單位.}$

$$\mathrm{l\:=\:2h(l\:+\:b)\:平方單位是長方體側表面積}$$

其中，

l = 長度，

b = 寬度，

h = 高度，

S = 總表面積，以及

L = 側表面積

長方體的體積

長方體的體積用於確定它佔據的空間量。長方體的長、寬和高決定了它的體積。因此，更改這些值中的任何一個都會更改形狀的體積。長方體的體積以立方單位表示。因此，以下是計算長方體體積的公式 -

因此，$\mathrm{長方體的體積，V\:=\:l\times\:b\times\:h\:=\:lbh\:立方單位.}$

其中，

l = 長度

b = 寬度，以及

h = 高度

長方體的性質

長方體的關鍵特徵使其易於識別。它們是 -

• 長方體有 6 個面、8 個頂點和 12 條邊

• 長方體的頂點處僅形成直角

• 所有面的形狀都是矩形。

• 可以在長方體的每個面上畫兩條對角線。

• 彼此相對的邊平行。

• 長方體具有以下尺寸：長、寬和高。

一些現實生活中的長方體示例

我們已經編制了一些現實世界中長方體的列表。檢視列表，看看您在外出時是否可以找到其中任何一個，並嘗試看看您是否有自己的示例要新增

• 建築物 - 當您在城鎮或大都市周圍散步時，請檢視建築物。您會注意到其中許多具有長方體的形狀。

• 盒子 - 當您瀏覽超市、挑選一雙新鞋或拆開禮物時，請注意盒子。您會發現，大多數盒子都是長方體形狀的。

結論

在本教程中，我們學習了長方體以及長方體的性質。長方體是矩形稜柱。長方體的體積由 $\mathrm{l\times\:b\times\:h}$給出，側表面積由 $\mathrm{2(l\:+\:b)\times\:h}$給出，總表面積由 $\mathrm{2(lb\:+\:bh\:+\:hl)}$給出。

常見問題

1. 尺寸為 7×6×3 單位的長方體的對角線長度是多少？

長方體公式的對角線長度為 $\mathrm{\sqrt{(l^{2}\:+\:w^{2}\:+\:h^{2})}}$ 單位。

假設長度 (l) = 7，寬度 (w) = 6，高度 (h) = 3

因此，對角線的長度等於 $\mathrm{\sqrt{(7^{2}\:+\:6^{2}\:+\:3^{2})}}$ 單位。

因此，$\mathrm{對角線的長度\:=\:\sqrt{(7^{2}\:+\:6^{2}\:+\:3^{2})}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\sqrt{(49\:+\:36\:+\:9)}\:單位\:=\:\sqrt{94}\:單位}$

2. 大衛有一個長方體盒子，尺寸為 12×7×5。盒子的體積是多少？

長方體體積 = 長度、寬度和高度，以立方單位表示。透過更改提供的變數，我們得到

$\mathrm{體積\:=\:12\times\:7\times\:5\:立方英寸}$

$\mathrm{體積\:=\:420\:立方英寸}$

3. 確定長方體的表面積。其尺寸為 8×6×4 單位？

長方體表面積的公式為 2(lw + wh + lh) 平方單位。讓我們使用提供的尺寸計算長度 (l) 為 8 單位、寬度 (w) 為 6 單位和高度 (h) 為 4 單位。

因此，表面積 $\mathrm{=\:2\:\lbrace\:(8\times\:6)\:+\:(6\times\:4)\:+\:(8\times\:4)\rbrace}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:2(48\:+\:24\:+\:32)\:平方單位\:=\:2(104)\:=\:208\:平方單位.}$

4. 長方體和矩形稜柱有什麼區別？

由於兩者都具有 6 個矩形面、8 個頂點和 12 條邊，因此長方體和矩形稜柱是相同的。此外，兩者都具有盒狀外觀。