晶體場理論

---

引言

在本教程中，讓我們學習晶體場理論。在深入瞭解晶體場理論的定義之前，讓我們先整體瞭解一些術語，這將有助於我們更好地理解這個概念。

簡併能級

如果多個量子力學態具有相同的能級，則這些能級被稱為簡併能級。

過渡金屬

過渡金屬具有空的d軌道。d軌道分裂成兩個能級子能級，電子在這些能級之間移動賦予了它們獨特的性質。

一些過渡金屬的例子包括銅、鐵、錳等。

配體

能夠向中心金屬原子提供一對電子並與其形成配位鍵的原子、分子或離子。

現在讓我們概述一下晶體場理論：

“過渡金屬和配體之間的相互作用源於帶正電的金屬陽離子和配體非鍵合電子上的負電荷之間的吸引力”。

對於陰離子，配體被認為是點電荷；對於中性分子，配體被認為是點偶極子。在孤立的氣態金屬原子中，五個d軌道具有相同的能量，即它們是簡併的。如果一個球形平衡的負電荷場包圍著金屬原子，則這種簡併性將保持不變。然而，當這個負電場是由配合物中的配體產生時，它變得不平衡，d軌道的簡併性被解除，導致d軌道分裂。

分離的形式取決於晶體場的性質。

晶體場分裂成

• 八面體配位實體

• 四面體配位實體。

晶體場分裂成八面體配位實體

• 八面體配合物需要六個配體。

• 具有六對電子或配體或鍵的分子化合物稱為八面體。

• Octa 表示八。

• 好奇為什麼具有六對電子或鍵的分子化合物被稱為八面體？

  因為它的形狀有8個面。

圖1：六個配體

包含d軌道的金屬，即$\mathrm{dxy,\:dyz,\:dzx,\:dx^2-dy^2,\:Dz^2}$，被稱為5d軌道。這些存在於金屬中的5d軌道被稱為簡併能級。這是因為所有d軌道都具有相同的能級。

現在，讓我們看看d軌道的結構：

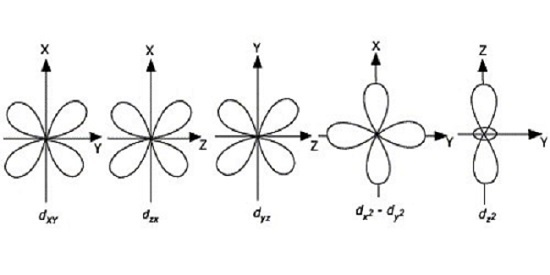
圖2：d軌道的結構

如上圖所示：

• 在dxy中 - 瓣位於x軸和y軸之間

• 在dyz中 - 瓣位於y軸和z軸之間

• 在dzx中 - 瓣位於z軸和x軸之間

• 在$\mathrm{dx^2 – dy^2}$中 - 瓣位於x軸和y軸上

• 在$\mathrm{dz^2}$中 - 瓣位於z軸上

dxy、dyz、dzx被稱為$\mathrm{t_{2g}}$軌道，而$\mathrm{dx^2-dy^2,\:Dz^2}$被稱為eg軌道。請參見下圖以更好地理解。

*請注意，所有d軌道都具有相同的能級

圖3：t2g軌道和eg軌道

如果我們看到像$\mathrm{[Co(CN_6)]^{3-}\: and\:[CoF_6]^{3–}}$這樣的配合物，氟離子$\mathrm{(F_6)}$和氰化物離子$\mathrm{(CN_6)}$接近金屬形成配合物。

當配體接近金屬形成配合物時，配體和金屬之間會發生排斥。每當發生排斥時，d軌道就會失去其簡併性。當它失去簡併性時，它就會變成非簡併d軌道或球形晶體場中的平均能量d軌道。

這些非簡併d軌道分裂成兩組。

• eg組

• $\mathrm{t_{2g}}$組。

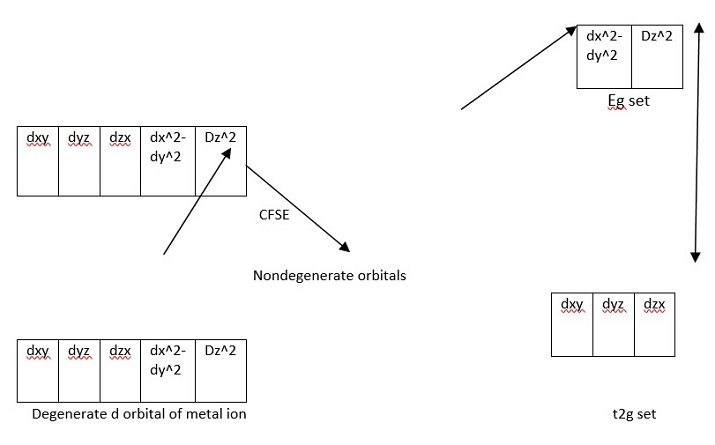
圖4：八面體配合物

在八面體配合物的情況下，配體沿軸接近。如**圖2**所示，eg組沿軸線方向。由於配體和eg瓣沿軸線方向，因此eg組中的排斥力較大，能級升高。由於t2g組經歷的排斥力較小，因此它們的能級降低。這種分裂被稱為晶體場分裂能(CFSE)或晶體場穩定化能。

eg組和$\mathrm{t_{2g}}$組之間的能量差被稱為晶體場分裂能，表示為$\mathrm{\Delta o}$。

這裡：

∆代表晶體場分裂能，

O代表八面體配合物。

因此：

eg的能級升高了+3/5∆o = eg的值為+0.6∆o

$\mathrm{t_{2g}}$的能級降低了-2/5∆o = $\mathrm{t_{2g}}$的值為-0.4∆o

晶體場分裂成四面體配位實體

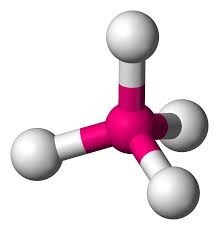
圖5：四面體配合物

在四面體配合物的情況下，金屬和配體之間形成的鍵數為四個。因此，配位數也是四個。

對於四面體配合物，配體跨軌道接近。

由於配體和t2瓣跨軸線方向，因此t2組中的排斥力較大，能級升高。由於e組經歷的排斥力較小，因此它們的能級降低，如下圖6所示。

圖6：四面體配合物

t2組和e組之間的能量差表示為∆t

其中，t代表四面體配合物。

t2的能級升高了+2/5∆o = eg的值為+0.4∆t

e的能級降低了-3/5∆t = t2g的值為-0.6∆t

（注：由於四面體配合物缺乏對稱性，“g”下標不用於能級）

常見問題

Q1. 晶體場理論是誰在何時發現的？

A1. 物理學家漢斯·貝特 (Hans Bethe) 於 1929 年為晶體固體發展了晶體場理論 (CFT)。

Q2. 晶體場理論的優點是什麼？

A2.

• 該理論可以解釋配合物的穩定性。晶體場分裂能越大，穩定性越高。

• 該理論可以解釋配合物的顏色和光譜。

• 該理論解釋了配合物的磁性。

Q3. CFT 的應用是什麼？

A3. 可以使用晶體場理論 (CFT) 預測配位化合物的顏色。瞭解顏色可以有很多有用的應用，例如在紡織工業中為染料創造顏料。