破解 RSA 密碼

使用小素數有可能破解 RSA 密碼，但如果它與大數字一起使用，則認為不可能破解。指定破解 RSA 密碼困難的原因如下 −

• 蠻力攻擊不可行，因為有太多可能的金鑰需要處理。同樣，這會浪費大量時間。

• 字典攻擊不適用於 RSA 演算法，因為金鑰是數字的且其中不包含任何字元。

• 對字元進行頻率分析非常困難，因為單個加密塊表示各個字元。

• 沒有特定的數學技巧可以破解 RSA 密碼。

RSA 解密方程式為 −

M = C^d mod n

藉助小素數，我們可以嘗試破解 RSA 密碼，其示例程式碼如下 −

def p_and_q(n):
   data = []
   for i in range(2, n):
      if n % i == 0:
         data.append(i)
   return tuple(data)

def euler(p, q):
   return (p - 1) * (q - 1)

def private_index(e, euler_v):
   for i in range(2, euler_v):
      if i * e % euler_v == 1:
         return i

def decipher(d, n, c):
   return c ** d % n
	def main():
      e = int(input("input e: "))
      n = int(input("input n: "))
      c = int(input("input c: "))
      
      # t = 123
      # private key = (103, 143)
      p_and_q_v = p_and_q(n)
      # print("[p_and_q]: ", p_and_q_v)
      euler_v = euler(p_and_q_v[0], p_and_q_v[1])
      
      # print("[euler]: ", euler_v)
      d = private_index(e, euler_v)
      plain = decipher(d, n, c)
      print("plain: ", plain)
if __name__ == "__main__":
   main()

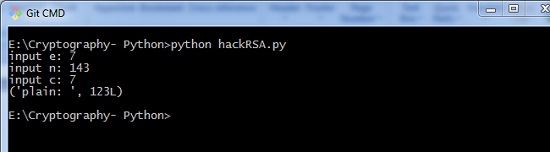
輸出

以上程式碼產生以下輸出 −