資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學圖的連通性
能否從一個頂點遍歷到圖的另一個頂點取決於圖的連線方式。連通性是圖論中的一個基本概念。連通性定義了圖是連通的還是不連通的。它根據邊和頂點有子主題，稱為邊連通性和頂點連通性。讓我們詳細討論它們。
連通性
如果**每對頂點之間都存在一條路徑**，則稱該圖是**連通的**。從每個頂點到任何其他頂點，都應該存在一些路徑可以遍歷。這就是圖的連通性。具有多個不連通頂點和邊的圖被稱為不連通圖。
示例1
在下面的圖中，可以從一個頂點遍歷到任何其他頂點。例如，可以使用路徑“a-b-e”從頂點“a”遍歷到頂點“e”。
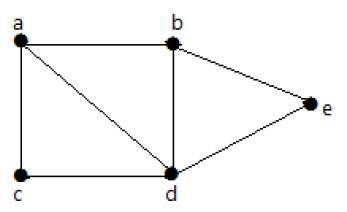
示例2
在下面的示例中，無法從頂點“a”遍歷到頂點“f”，因為它們之間不存在直接或間接的路徑。因此，它是一個不連通圖。
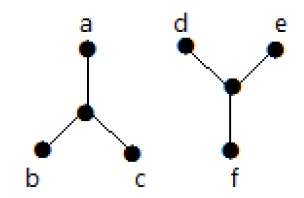
連通性型別
圖的連通性大致可以分為兩類：
邊連通性
頂點連通性
邊連通性
設“G”是一個連通圖。移除使得“G”不連通的最小邊數稱為G的邊連通性。
**符號** − λ(G)
換句話說，**G的最小割集中的邊數**稱為G的邊連通性。
如果“G”有一條割邊，則*λ(G)*為1。（G的邊連通性。）
示例
看一下下面的圖。透過移除兩條最小邊，連通圖變得不連通。因此，它的邊連通性(λ(G))為2。
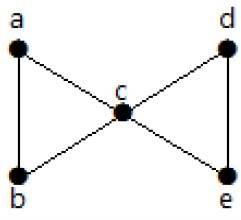
這裡有四種透過移除兩條邊來斷開圖連線的方法：
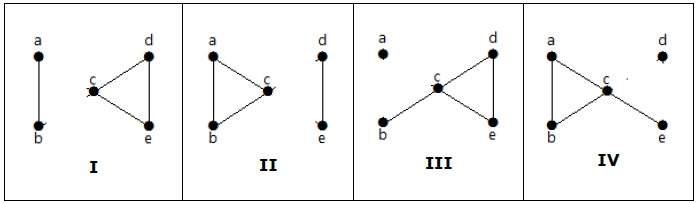
頂點連通性
設“G”是一個連通圖。移除使得“G”變得不連通或將“G”簡化為平凡圖的最小頂點數稱為它的頂點連通性。
**符號** − K(G)
示例
在上圖中，移除頂點“e”和“i”會使圖不連通。
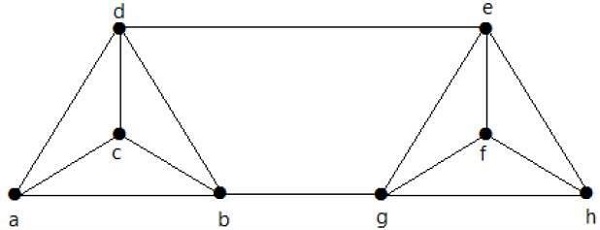
如果G有一個割頂，則K(G) = 1。
**符號** − 對於任何連通圖G，
K(G) ≤ λ(G) ≤ δ(G)
頂點連通性 (K(G))，邊連通性 (λ(G))，G 的最小度數 (δ(G))。
示例
計算以下圖的λ(G)和K(G)：
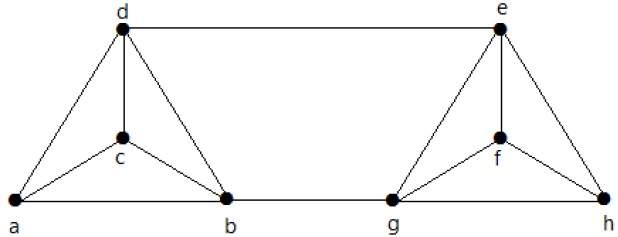
解答
從圖中，
δ(G) = 3
K(G) ≤ λ(G) ≤ δ(G) = 3 (1)
K(G) ≥ 2 (2)
刪除邊 {d, e} 和 {b, h}，我們可以斷開 G 的連線。
因此，
λ(G) = 2
2 ≤ λ(G) ≤ δ(G) = 2 (3)
從 (2) 和 (3) 可知，頂點連通性 K(G) = 2
423 次瀏覽
