連通性、距離和生成樹

生成樹

一個簡單的定義是，樹是一個與之關聯的無環連通圖，其中一個環允許我們從一個節點返回到自身而不重複任何邊。

連通圖 G 的生成樹定義為包含 G 所有頂點的樹。

生成樹常用於網際網路路由演算法。在網際網路中，計算機（節點）通常透過許多冗餘的物理連線連線。

圖中生成樹的總數。如果一個圖是一個具有 n 個頂點的完全圖，則生成樹的總數為 n^(n-2)

其中 n 表示圖中節點的數量。在完全圖中，該任務等價於計算具有 n 個節點的不同標記樹，這可以使用凱萊公式。

連通性

在數學和計算機科學中，連通性是圖論的基本概念之一

它需要移除的最少元素（節點或邊）數量，以將剩餘節點分離成孤立的子圖。

它與網路流問題的理論密切相關。

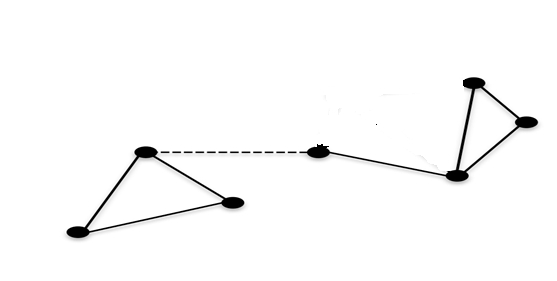
當虛線邊被移除時，此圖變得不連通。

頂點連通性。圖的頂點連通性是刪除其會導致圖斷開連線的最少節點數。

頂點連通性有時表示為“點連通性”或簡稱為“連通性”。

邊連通性。從圖中刪除其會導致圖斷開連線的最少邊數，也稱為線連通性。

不連通圖的邊連通性為 0，而與圖橋關聯的連通圖的邊連通性為 1。

距離

兩個節點之間的距離可以用最低公共祖先來計算。以下是公式。

Dist(d1, d2) = Dist(root, d1) + Dist(root, d2) - 2*Dist(root, lca)
'd1' and 'd2' are the two given keys
'root' is root of given Binary Tree.
'lca' is lowest common ancestor of d1 and d2
Dist(d1, d2) is the distance between d1 and d2.

Arnab Chakraborty

更新於： 2020年1月2日

487 次檢視

開啟你的 職業生涯

透過完成課程獲得認證

開始學習