圓錐曲線

---

簡介

• 當一個固體表面如圓錐體被平面切割時，它會形成不同的截面，稱為圓錐曲線。

• 根據平面與圓錐軸線相交的角度不同，圓錐曲線可以是圓、橢圓、拋物線和雙曲線。

• 圓和橢圓是封閉的截面，而拋物線和雙曲線不是封閉的，它們的曲線延伸到無窮大。

圓錐截面的定義

• 當一個二維平面與一個三維直圓錐相交時，在平面上形成的截面稱為圓錐曲線。

• 平面以不同的角度與圓錐相交，形成不同的圓錐曲線，如圓、拋物線、橢圓和雙曲線。不同的圓錐曲線有不同的引數和方程。

圓錐曲線的引數

除了焦點、準線和離心率之外，圓錐曲線還有其他一些引數。

• 準線 - 它是一條平行於準線的直線，並且必須經過圓錐曲線的焦點，稱為圓錐曲線的準線。

• 焦引數 - 圓錐曲線焦點到其對應準線的距離稱為焦引數。

• 主軸 - 經過拋物線的焦點和準線的直線，或連線雙曲線和橢圓兩個焦點的直線稱為主軸。其中點是圓錐曲線的中心。

• 線性離心率 - 圓錐曲線中心到焦點的距離稱為圓錐曲線的線性離心率。

• 長軸 - 經過中心的弦中最長的稱為長軸。

• 短軸 - 經過中心的弦中最短的稱為短軸。

焦點、離心率和準線

• 準線 - 平面上一個動點到一個定點和一條定直線的距離的軌跡是定義圓錐曲線的另一種方法。這條定直線稱為圓錐曲線的準線。

• 焦點 - 這個定點稱為圓錐曲線的焦點。圓錐曲線的焦點不在其準線上。

• 離心率 - 考慮圓錐曲線上的一個點 P。點 P 到焦點的距離與點 P 到準線的垂直距離之比稱為離心率，對於給定的圓錐曲線，它是常數。用'e'表示。

• 如果圓錐曲線的離心率為零，則它是圓。

• 如果圓錐曲線的離心率嚴格位於零和一之間，則它是橢圓。

• 如果圓錐曲線的離心率為一，則它是拋物線。

• 如果圓錐曲線的離心率大於一，則它是雙曲線。

圓錐的截面

重要的圓錐曲線有圓、拋物線、橢圓和雙曲線。

• 圓 - 當平面與圓錐的軸線成90度角切割時，就會形成一個名為圓的圓錐曲線。

• 橢圓 - 當平面與圓錐的軸線成小於90度但大於圓錐半頂角的角度切割時，就會形成一個名為橢圓的圓錐曲線。

• 拋物線 - 當平面與圓錐的軸線成等於圓錐半頂角的角度切割時，就會形成一個名為拋物線的圓錐曲線。

• 雙曲線 - 當平面與圓錐的軸線成小於圓錐半頂角的角度切割時，就會形成一個名為雙曲線的圓錐曲線。

圓錐截面的方程

四個圓錐曲線圓、橢圓、拋物線和雙曲線都有各自的方程。

圓

圓是一組到一個稱為圓心的點的距離相等的點的軌跡。這個距離稱為圓的半徑。根據距離，可以推匯出圓的方程。

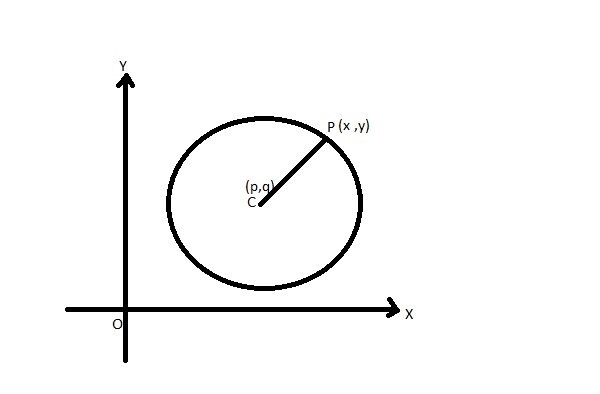
考慮一個圓心為 (p, q)，圓上有一點 P (x, y) 的圓。圓的半徑為 r。

點 P 與圓心的距離等於半徑 r。

$\mathrm{(x\:-\:p)^{2}\:+\:(y\:-\:q)^{2}\:=\:r^{2}}$

橢圓

橢圓是一組到兩個定點（稱為焦點）的距離之和相等的點的軌跡。

考慮一個圓心為 (p, q)，橢圓上任意一點 (x, y)，長軸為 x 軸，a 為半長軸，b 為半短軸的橢圓。

$$\mathrm{\frac{(x\:-\:p)^{2}}{a^{2}}\:+\:\frac{(y\:-\:q)^{2}}{b^{2}}\:=\:1}$$

拋物線

拋物線是一組到焦點和到準線的垂直距離相等的點的軌跡。

考慮一個沿 x 軸，圓心為 (p, q)，拋物線上一點 P (x, y)，焦點在 (p + a, q) 的拋物線。

$$\mathrm{(y\:-\:p)^{2}\:=4a\:(x\:-\:p)}$$

雙曲線

雙曲線是一組到兩個定點（稱為焦點）的距離之差相等的點的軌跡。

考慮一個沿 x 軸，圓心為 (p, q)，雙曲線上任意一點 (x, y)，a 為半實軸，b 為半虛軸的雙曲線。

$$\mathrm{\frac{(x\:-\:p)^{2}}{a^{2}}\:-\:\frac{(y\:-\:q)^{2}}{b^{2}}\:=\:1}$$

示例

• 已知圓心為 (2, 3)，圓上有一點 P (x, y)，圓的半徑為 4cm，求圓的方程？

$\mathrm{(x\:-\:2)^{2}\:+\:(y\:-\:3)^{2}\:=\:4^{2}}$

• 已知橢圓的方程為 $\mathrm{\frac{(x\:-\:1)^{2}}{16}\:+\:\frac{(y\:-\:2)^{2}}{9}\:=\:1}$，求橢圓的圓心、半長軸長度和半短軸長度？

將給定方程與 $\mathrm{\frac{(x\:-\:p)^{2}}{a^{2}}\:+\:\frac{(y\:-\:q)^{2}}{b^{2}}\:=\:1}$ 進行比較，橢圓的圓心等於 (1, 2)。

$\mathrm{a^{2}\:=\:16\Longrightarrow\:a\:=\:4\:,\:b^{2}\:=\:9\Longrightarrow\:b\:=\:3}$

結論

在本教程中，我們學習了圓錐曲線、其引數（如焦點、離心率、準線）、圓錐的不同截面（如圓、橢圓、拋物線、雙曲線）及其方程。

常見問題解答

1. 以原點為中心的沿 x 軸的拋物線的方程是什麼？

$\mathrm{y^{2}\:=\:4ax}$ 是以原點為中心的拋物線的方程。

2. 以原點為中心的圓的方程是什麼？

如果原點是圓的圓心，則圓的方程是 $\mathrm{(x)^{2}\:+\:(y)^{2}\:=\:r^{2}}$

3. 圓錐曲線為雙曲線的離心率條件是什麼？

對於圓錐曲線為雙曲線，其離心率必須大於一。

4. 已知雙曲線圓心為 (-1, 4)，雙曲線上有一點 P (x, y)，a = 5，b = 3，求雙曲線的方程？

雙曲線的方程是 $\mathrm{\frac{(x\:+\:1)^{2}}{25}\:-\:\frac{(y\:-\:4)^{2}}{9}\:=\:1}$

5. 以原點為中心的沿 y 軸的拋物線的方程是什麼？

$\mathrm{x^{2}\:=\:4ay}$ 是以原點為中心的拋物線的方程。