迴路秩

設 G 為一個具有 n 個頂點和 m 條邊的連通圖。G 的生成樹 T 包含 (n-1) 條邊。

因此，為了得到生成樹，你需要從 G 中刪除的邊的數量 = m-(n-1)，這稱為 G 的迴路秩。

這個公式是正確的，因為在生成樹中你需要有 'n-1' 條邊。在 m 條邊中，你需要在圖中保留 'n–1' 條邊。

因此，從 m 中刪除 'n–1' 條邊得到需要從圖中刪除的邊，以獲得不形成環的生成樹。

示例

檢視以下圖形 -

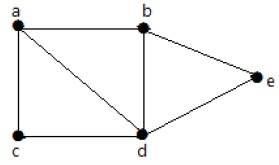
對於上面示例中給出的圖，你有 m=7 條邊和 n=5 個頂點。

那麼迴路秩為

G = m – (n – 1)
= 7 – (5 – 1)
= 3

示例

設 G 為一個具有六個頂點的連通圖，每個頂點的度數為三。求 G 的迴路秩。

根據頂點度數之和定理，

6 × 3 = 2|E|

|E| = 9

迴路秩 = |E| – (|V| – 1)

= 9 – (6 – 1) = 4

Mahesh Parahar

更新於: 2019年8月23日

824 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始學習