檢查根據給定條件從陣列構建的圖是否包含迴圈

簡介

在圖論中，確定根據陣列構建並滿足某些條件的圖是否包含迴圈是一項非常重要的任務。圖是一種抽象的方式來表示事物之間的連線關係。它被廣泛應用於各種領域，例如計算機網路和社交網路。本文討論了圖構建的條件、BFS 和 DFS 演算法，以及逐步指導如何識別無向圖中的迴圈。

圖的陣列表示

圖論中基於陣列的方法將頂點和邊儲存在陣列中，這使得它們易於操作並在演算法中使用。從空圖開始，根據陣列中的資訊逐一新增頂點和邊，是進一步探索的基礎，例如迴圈檢測，這對於理解圖的連線方式以及是否存在任何迴圈至關重要。

圖構建的條件

給定條件的解釋

  • 圖是從陣列構建的，其中陣列表示一組頂點及其連線或邊。

  • 陣列的每個元素對應圖中的一個頂點。

  • 陣列中每個元素的值指示它連線到的頂點的索引（其相鄰頂點）。

  • 陣列的索引表示頂點本身，其對應值表示它連線到的頂點。

驗證圖構建的條件

  • 在構建圖之前，檢查陣列是否有效並滿足所需的條件。

  • 確保陣列非空，並至少包含一個元素以建立頂點。

  • 驗證陣列是否僅包含非負整數，因為負值或無效資料不能表示有效的頂點或邊。

  • 確保陣列索引在適當的範圍內。它們應該從 0 到 n-1，其中 n 是圖中頂點的總數。

  • 確認陣列中的值（連線）也在 0 到 n-1 的有效範圍內，確保它們對應於現有的頂點。

  • 檢查是否存在任何重複連線或自環，因為它們違反了有效圖的條件。

  • 驗證是否存在任何缺失的連線，這意味著所有頂點都連線以形成一個完整的圖或一個連通分量。

DFS 和 BFS 演算法

  • 深度優先搜尋 (DFS) 用於透過儘可能深入地遍歷每個分支來探索圖的頂點和邊，然後再返回。

虛擬碼

procedure DFS(graph, start_vertex, visited)
   if start_vertex is not in visited:
      mark start_vertex as visited
      process start_vertex (e.g., check for cycles)
      for each neighbor in graph[start_vertex]:
      if neighbor is not in visited:
      DFS(graph, neighbor, visited)
   end if
end procedure
    pocedure DFS_Traversal(graph)
    visited = empty set
      for each vertex in graph:
      if vertex is not in visited:
         DFS(graph, vertex, visited)
   end for
end procedure

  • 廣度優先搜尋 (BFS) 是一種圖遍歷演算法，它一次遍歷圖的所有頂點一層。

虛擬碼

procedure BFS(graph, start_vertex):
   create an empty queue Q
   create a set visited to keep track of visited vertices
   
   enqueue start_vertex into Q
   add start_vertex to visited set
   
   while Q is not empty:
      current_vertex = dequeue from Q
      for each neighbor_vertex of current_vertex:
         if neighbor_vertex is not in visited set:
            enqueue neighbor_vertex into Q
            add neighbor_vertex to visited set
      else:
         // A cycle is detected, return true
         return true
      // No cycle found, return false
      return false

複雜度

  • 時間複雜度

    • BFS 和 DFS 的時間複雜度均為 O(V + E)，其中 V 是頂點的數量，E 是邊的數量。

  • 空間複雜度

    • BFS 和 DFS 的時間複雜度為 O(V)。

迴圈檢測的逐步過程

讓我們考慮一個帶有圖的示例。

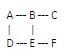
  • 從一個空集開始，用於跟蹤已訪問的頂點。

Visited set: {}

  • 選擇一個任意頂點作為迴圈檢測過程的起點。讓我們選擇頂點 A。

Visited set: {A}
Current Vertex: A

  • 檢查當前頂點 (A) 的相鄰頂點。在本例中，A 的鄰居是 B 和 D。將它們新增到已訪問集合中，並將 A 識別為它們的父節點。

Visited set: {A, B, D}
Current Vertex: A
Parent of B: A
Parent of D: A

  • B 是已訪問集合中的下一個已訪問頂點。

Visited set: {A, B, D}
Current Vertex: B
Parent of B: A

  • 發現 B 的鄰居。B 的直接鄰居是 A、C 和 E。A 已經在已訪問頂點集中，但它不是 B 的父節點，因此它不構成迴圈。

Visited set: {A, B, D, C, E}
Current Vertex: B

  • 繼續下一個已訪問頂點，即 D。

Visited set: {A, B, D, C, E}
Current Vertex: D
Parent of D: A

  • 發現 D 的熟人。A 和 E 是 D 的最近鄰居。由於 A 已經包含在已訪問集合中並且是 D 的父節點，因此必須存在一條邊 (D -> A) 將 D 連線到其父節點。這表明圖包含一個迴圈。

Cycle detected! There is an edge (D -> A) forming a cycle

流程到此結束，我們已成功使用 BFS 檢測到圖中的迴圈，即 (A->B->E->D->A)。

結論

總之，能夠根據給定條件從陣列構建的圖中找到迴圈對於許多應用程式來說非常重要。無論您使用 DFS 還是 BFS，此過程都有助於發現可能的迴圈並解決涉及網路、電路和關係的現實世界問題。有效的迴圈檢測可以提高演算法的速度並確保資料的正確性。

更新於: 2023年7月28日

137 次瀏覽

開啟你的 職業生涯

透過完成課程獲得認證

開始
廣告