資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學迷宮中老鼠問題 - 回溯法-2？
迷宮中的老鼠也是一個利用回溯法的流行問題。
迷宮是一個二維矩陣，其中一些單元格是被阻塞的。其中一個單元格是起始單元格，我們必須從那裡開始。另一個是目標單元格，我們必須到達那裡。我們必須找到一條從起始單元格到目標單元格的路徑，而不會進入任何被阻塞的單元格。下面顯示的是一個未解迷宮的圖片。
這是它的解決方案。
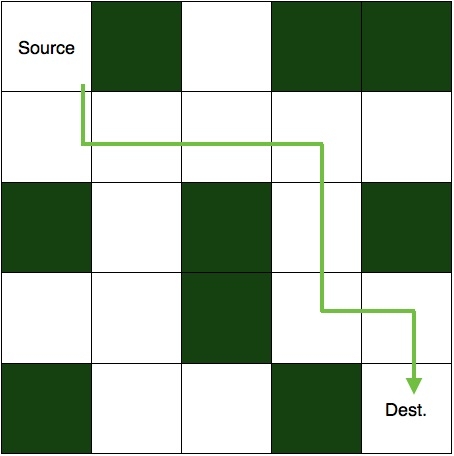
為了解決這個難題，我們首先從起始單元格開始，並向路徑未被阻塞的方向移動。如果所走的路徑使我們到達目標，則難題得到解決。否則，我們將返回並改變我們所走路徑的方向。我們也將在我們的程式碼中實現相同的邏輯。
Input:
maze[][] = {
{0,1,0,1,1},
{0,0,0,0,0},
{1,0,1,0,1},
{0,0,1,0,0},
{1,0,0,1,0}}
Output:
1 0 0 0 0
1 1 1 1 0
0 0 0 1 0
0 0 0 1 1
0 0 0 0 1解釋
首先，我們將建立一個矩陣來表示迷宮，矩陣的元素將是0或1。1表示被阻塞的單元格，0表示我們可以移動的單元格。上面所示迷宮的矩陣是
0 1 0 1 1 0 0 0 0 0 1 0 1 0 1 0 0 1 0 0 1 0 0 1 0
現在，我們將建立一個相同維度的另一個矩陣來儲存解決方案。它的元素也將是0或1。1表示我們路徑中的單元格，其餘單元格為0。表示解決方案的矩陣是
1 0 0 0 0 1 1 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1
因此，我們現在有了我們的矩陣。接下來，我們將找到從起始單元格到目標單元格的路徑，我們將採取的步驟是
檢查當前單元格，如果它是目標單元格，則難題已解決。
如果不是，我們將嘗試向下移動，看看我們能否向下移動（要移動到一個單元格，它必須是空的並且不在路徑中）。
如果我們可以移動到那裡，我們將繼續沿著路徑移動到下一個下方的單元格。
如果不是，我們將嘗試移動到右邊的單元格。如果它被阻塞或已被佔用，我們將向上移動。
同樣，如果我們也無法向上移動，我們將簡單地移動到左邊的單元格。
如果四個移動（下、右、上或左）都不可能，我們將簡單地返回並更改當前路徑（回溯）。
因此，總結一下，我們嘗試從當前單元格移動到另一個單元格（下、右、上和左），如果沒有任何移動可能，則返回並更改路徑方向到另一個單元格。
printsolution → 此函式只是列印解決方案矩陣。
solvemaze → 這是我們實現回溯演算法的實際函式。首先，我們檢查我們的單元格是否是目標單元格 if (r==SIZE-1) and (c==SIZE-1)。如果它是目標單元格，則我們的難題已經解決。如果不是，我們將檢查它是否是有效的移動單元格。有效的單元格必須在矩陣中，即索引必須在0到SIZE-1之間 r>=0 && c>=0 && r<SIZE；不得被阻塞 maze[r][c] == 0，並且不得在路徑 solution[r][c] == 0 中。如果這是一個有效的移動，那麼我們可以自由地進行移動並移動到下一個單元格。首先，我們將嘗試下方的單元格 if(solveMaze(r+1, c))。如果它沒有給我們解決方案，我們將移動到右邊的單元格，同樣地移動到上方的和左邊的單元格。如果所有單元格都未能給我們解決方案，我們將離開單元格 solution[r][c] = 0 並轉到其他單元格。
示例
#include <iostream>
using namespace std;
#define SIZE 5
//the maze problem
int maze[SIZE][SIZE] = {
{0,1,0,1,1},
{0,0,0,0,0},
{1,0,1,0,1},
{0,0,1,0,0},
{1,0,0,1,0}
};
//matrix to store the solution
int solution[SIZE][SIZE];
//function to print the solution matrix
void printsolution() {
int i,j;
for(i=0;i<SIZE;i++) {
for(j=0;j<SIZE;j++) {
printf("%d\t",solution[i][j]);
}
printf("
");
}
}
//function to solve the maze
//using backtracking
int solvemaze(int r, int c) {
//if destination is reached, maze is solved
//destination is the last cell(maze[SIZE-1][SIZE-1])
if((r==SIZE-1) && (c==SIZE-1) {
solution[r][c] = 1;
return 1;
}
//checking if we can visit in this cell or not
//the indices of the cell must be in (0,SIZE-1)
//and solution[r][c] == 0 is making sure that the cell is not already visited
//maze[r][c] == 0 is making sure that the cell is not blocked
if(r>=0 && c>=0 && r<SIZE && c<SIZE && solution[r][c] == 0 && maze[r][c] == 0){
//if safe to visit then visit the cell
solution[r][c] = 1;
//going down
if(solvemaze(r+1, c))
return 1;
//going right
if(solvemaze(r, c+1))
return 1;
//going up
if(solvemaze(r-1, c))
return 1;
//going left
if(solvemaze(r, c-1))
return 1;
//backtracking
solution[r][c] = 0;
return 0;
}
return 0;
}
int main() {
//making all elements of the solution matrix 0
int i,j;
for(i=0; i<SIZE; i++) {
for(j=0; j<SIZE; j++) {
solution[i][j] = 0;
}
}
if (solvemaze(0,0))
printsolution();
else
printf("No solution
");
return 0;
}
3K+ 次瀏覽
