資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++ 中的 BK 樹簡介
BK 樹或 Burkhard 樹是一種資料結構形式，通常用於基於萊文斯坦距離執行拼寫檢查。它也用於字串匹配，自動更正功能可以使用這種資料結構。假設我們在字典中有一些單詞，我們需要檢查其他一些單詞是否存在拼寫錯誤。我們需要有一個單詞集合，這些單詞接近於要檢查拼寫給定的單詞。例如，如果我們有單詞“uck”，正確的單詞可以是（truck、duck、duck、suck）。因此，拼寫錯誤可以透過刪除一個單詞或新增一個新單詞來更正，用合適的字母替換一個字母。使用編輯距離作為引數並使用字典檢查拼寫。
與所有其他樹一樣，BK 樹也由節點和邊組成。節點表示字典中的單詞。邊包含一些整數權重，這些權重為我們提供從一個節點到另一個節點的編輯距離資訊。
考慮一個包含單詞 {book, books, boo, cake, cape} 的字典 -
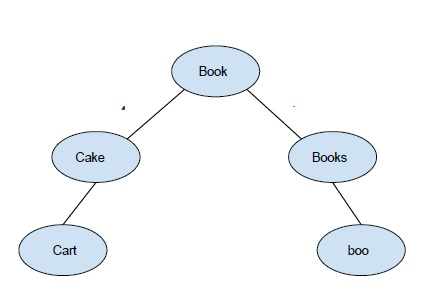
BK 樹
BK 樹中的每個節點都只有一個具有相同編輯距離的子節點。如果我們在插入節點時遇到一些編輯距離衝突，我們將傳播插入過程，直到我們得到正確的子節點。每個插入都從根節點開始，根節點可以是任何單詞。到目前為止，我們已經瞭解了什麼是 Bk 樹。現在讓我們看看如何找到正確的最接近的單詞。首先，我們需要設定容差值，此容差值只不過是我拼寫錯誤的單詞和正確單詞之間的最大編輯距離。
為了在容差範圍內找到合格的正確單詞，我們使用迭代過程。但這具有較高的複雜度，因此現在 BK 樹開始發揮作用，因為我們知道二叉樹中的每個節點都是根據其與父節點的編輯距離構建的。因此，我們可以直接從根節點到位於容差範圍內的特定節點。如果 TOL 是容差限制，並且當前節點與拼寫錯誤的節點的編輯距離為 dist。所以現在，我們只迭代那些編輯距離在範圍內的子節點。
[dist - TOL, dist+TOL]，這在很大程度上降低了複雜度。
示例
說明工作原理的程式 -
#include "bits/stdc++.h"
using namespace std;
#define MAXN 100
#define TOL 2
#define LEN 10
struct Node {
string word;
int next[2*LEN];
Node(string x):word(x){
for(int i=0; i<2*LEN; i++)
next[i] = 0;
}
Node() {}
};
Node RT;
Node tree[MAXN];
int ptr;
int min(int a, int b, int c) {
return min(a, min(b, c));
}
int editDistance(string& a,string& b) {
int m = a.length(), n = b.length();
int dp[m+1][n+1];
for (int i=0; i<=m; i++)
dp[i][0] = i;
for (int j=0; j<=n; j++)
dp[0][j] = j;
for (int i=1; i<=m; i++) {
for (int j=1; j<=n; j++) {
if (a[i-1] != b[j-1])
dp[i][j] = min( 1 + dp[i-1][j], 1 + dp[i][j-1], 1 + dp[i-1][j-1] );
else
dp[i][j] = dp[i-1][j-1];
}
}
return dp[m][n];
}
void insertValue(Node& root,Node& curr) {
if (root.word == "" ){
root = curr;
return;
}
int dist = editDistance(curr.word,root.word);
if (tree[root.next[dist]].word == ""){
ptr++;
tree[ptr] = curr;
root.next[dist] = ptr;
}
else{
insertValue(tree[root.next[dist]],curr);
}
}
vector <string> findCorrectSuggestions(Node& root,string& s){
vector <string> corrections;
if (root.word == "")
return corrections;
int dist = editDistance(root.word,s);
if (dist <= TOL) corrections.push_back(root.word);
int start = dist - TOL;
if (start < 0)
start = 1;
while (start < dist + TOL){
vector <string> temp = findCorrectSuggestions(tree[root.next[start]],s);
for (auto i : temp)
corrections.push_back(i);
start++;
}
return corrections;
}
int main(){
string dictionary[] = {"book","cake","cart","books", "boo" };
ptr = 0;
int size = sizeof(dictionary)/sizeof(string);
for(int i=0; i<size; i++){
Node tmp = Node(dictionary[i]);
insertValue(RT,tmp);
}
string word1 = "ok";
string word2 = "ke";
vector <string> match = findCorrectSuggestions(RT,word1);
cout<<"Correct words suggestions from dictionary for : "<<word1<<endl;
for (auto correctWords : match)
cout<<correctWords<<endl;
match = findCorrectSuggestions(RT,word2);
cout<<"Correct words suggestions from dictionary for : "<<word2<<endl;
for (auto correctWords : match)
cout<<correctWords<<endl;
return 0;
}輸出
Correct words suggestions from dictionary for : ok book boo Correct words suggestions from dictionary for : ke cake
244 次瀏覽
