資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服飾學
法學C++ 中的二叉樹中的攝像頭
假設我們有一棵二叉樹；我們在樹節點上放置攝像頭。現在，節點上的每個攝像頭都可以監控其父節點、自身及其子節點。我們必須找到監測樹的所有節點所需的攝像頭最低數量。
因此，如果輸入如下所示 -
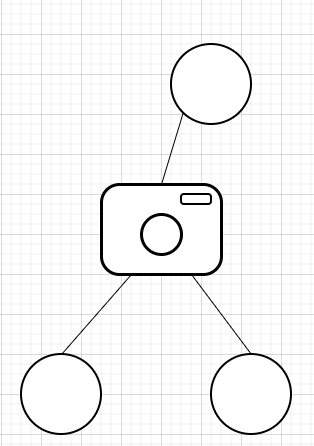
那麼輸出將為 1，因為只需要一個攝像頭就可以追蹤所有。
要解決這個問題，我們將遵循以下步驟 -
定義名為 covered 的集合，型別為 TreeNode（樹節點具有 left、right 和 data 欄位）
定義函式 solve()，這將採用 node、parent，
如果 node 為 null，則 -
返回
solve(node 的左側、node)
solve(node 的右側、node)
如果 (parent 與 NULL 相同並且 (node、node 的左側、node 的右側) 沒有被覆蓋，則 -
(增加 ans 為 1)
將 node 插入到 covered 中
將 node 的左側插入到 covered 中
將 node 的右側插入到 covered 中
將 parent 插入到 covered 中
在主要方法中執行以下操作，
ans := 0
在覆蓋中插入 NULL
solve(根, NULL)
返回 ans
讓我們檢視以下實現，以獲得更好的理解 -
示例
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = NULL;
right = NULL;
}
};
class Solution {
public:
set<TreeNode*> covered;
int ans;
int minCameraCover(TreeNode* root){
covered.clear();
ans = 0;
covered.insert(NULL);
solve(root, NULL);
return ans;
}
void solve(TreeNode* node, TreeNode* parent){
if (!node)
return;
solve(node->left, node);
solve(node->right, node);
if ((parent == NULL && covered.find(node) == covered.end())
|| covered.find(node->left) == covered.end() || covered.find(node-
>right) == covered.end()) {
ans++;
covered.insert(node);
covered.insert(node->left);
covered.insert(node->right);
covered.insert(parent);
}
}
};
main(){
Solution ob;
TreeNode *root = new TreeNode(1);
root->left = new TreeNode(1);
root->left->left = new TreeNode(1); root->left->right = new
TreeNode(1);
cout << (ob.minCameraCover(root));
}輸入
[1,1,NULL,1,1]
輸出
1
更新於:08-06-2020
201 次瀏覽
廣告