資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究C++ 中的二叉樹傾斜
假設我們有一個二叉樹的根節點，任務是找到並返回每個節點的傾斜度之和。
二叉樹的**傾斜度**是指透過在每一層找到左子樹和右子樹中子節點的絕對差來構建二叉樹。在某一層，如果節點沒有子節點，我們只需用零替換該節點來計算傾斜度。
示例
輸入
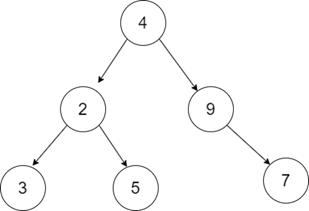
輸出：15
解釋：找到給定二叉樹每一層的傾斜度，
節點 3 的傾斜度 = 0
節點 5 的傾斜度 = 0
節點 7 的傾斜度 = 0
節點 2 的傾斜度 = abs(3-5)= 2
節點 9 的傾斜度 = abs(0-7)= 7
節點 4 的傾斜度 = abs((3+5+2)- (9+7))= 6
所有節點的傾斜度之和 = 2+7+6= 15
解決此問題的方法
解決此特定問題的一種簡單方法是使用後序廣度優先搜尋遍歷。
在遍歷二叉樹時，我們將嘗試找到其左子樹然後是右子樹的所有節點的總和。找到總和後，我們將透過計算其左子樹和右子樹總和的絕對差來找到所有節點的傾斜度。
- 取一個二叉樹作為輸入。
- 一個整數函式 sumNodes(treenode*node) 獲取樹的根節點並返回左子樹和右子樹的總和。
- 一個整數函式 findTilt(treenode*root) 獲取根節點作為輸入引數並返回所有節點的傾斜度之和。
示例
#include<iostream>
using namespace std;
struct treenode {
int data;
treenode * left;
treenode * right;
};
struct treenode * createNode(int d) {
struct treenode * root = new treenode;
root -> data = d;
root -> left = NULL;
root -> right = NULL;
return root;
}
int sumNodes(treenode * root, int & sum) {
if (root == NULL) return 0;
int lsum = sumNodes(root -> left, sum);
int rsum = sumNodes(root -> right, sum);
sum += abs(lsum - rsum);
return lsum + rsum + root -> data;
}
int findTilt(treenode * root) {
int sum = 0;
if (root == NULL) {
return 0;
}
sumNodes(root, sum);
return sum;
}
int main() {
struct treenode * root = NULL;
root = createNode(4);
root -> left = createNode(2);
root -> right = createNode(9);
root -> left -> right = createNode(5);
root -> left -> left = createNode(3);
root -> right -> right = createNode(7);
cout << findTilt(root) << endl;
return 0;
}執行以上程式碼將生成以下輸出：
輸出
15
在給定的二叉樹中，樹每一層所有節點的傾斜度之和為 15。
更新於： 2021年2月23日
249 次檢視
廣告