資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++中的樹直徑
假設我們有一個無向樹；我們需要找到它的直徑——樹中最長路徑中的邊數就是該樹的直徑。這裡樹以邊列表的形式給出，其中edges[i] = [u, v]是節點u和v之間的雙向邊。每個節點的標籤都在集合{0, 1, ..., edges.length}中。所以如果圖是這樣的：
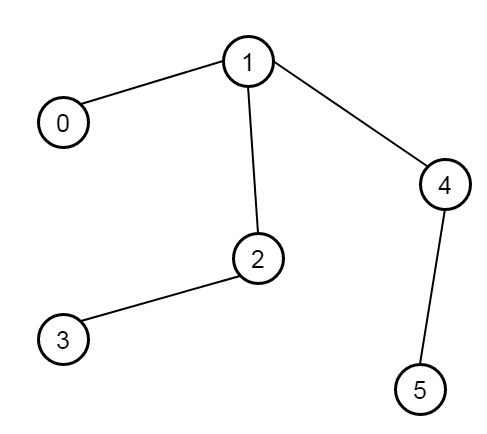
輸出將是4。
為了解決這個問題，我們將遵循以下步驟：
- 定義一個對映l
- 定義一個名為dfs()的方法。它將接受v、一個名為visited的陣列、圖和c。它的工作原理如下：
- visited[v] := true，設定ans := 0
- 對於範圍0到graph[v]大小的i
- 如果visited[graph[v, i]]為false，則
- ans := ans和dfs(graph[v, i], visited, graph, c + 1)中的最大值
- 如果visited[graph[v, i]]為false，則
- 如果c > best，則best := c且node := v
- 設定visited[v] := false
- 返回c和ans中的最大值
- 在主方法中，它將接受邊列表e
- n := e的大小，建立一個大小為n + 1的陣列graph
- 對於範圍0到n – 1的i
- 將e[i, 1]插入graph[e[i, 0]]中，並將e[i, 0]插入graph[e[i, 1]]中
- 建立兩個大小為n + 1的陣列visited和visited2，設定best := 0和node := 0
- 呼叫dfs(0, visited, graph)
- 返回dfs(node, visited2, graph)
示例(C++)
讓我們看看下面的實現，以便更好地理解：
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
class Solution {
public:
map <int ,int > l;
int best;
int node;
int dfs(int v, bool* visited, vector <int> graph[], int c = 0){
visited[v] = true;
int ans = 0;
for(int i = 0; i < graph[v].size(); i++){
if(!visited[graph[v][i]])ans = max(ans,dfs(graph[v][i], visited, graph, c+1));
}
if(c > best){
best = c;
node = v ;
}
visited[v] = false;
return max(c,ans);
}
int treeDiameter(vector<vector<int>>& e) {
int n = e.size();
vector <int> graph[n+1];
for(int i = 0; i < n; i++){
graph[e[i][0]].pb(e[i][1]);
graph[e[i][1]].pb(e[i][0]);
}
bool* visited = new bool[n+1]();
best = 0;
node = 0;
dfs(0, visited, graph);
bool* visited2 = new bool[n+1]();
return dfs(node, visited2, graph);
}
};
main(){
vector<vector<int>> v = {{0,1},{1,2},{2,3},{1,4},{4,5}};
Solution ob;
cout <<ob.treeDiameter(v);
}輸入
[[0,1],[1,2],[2,3],[1,4],[4,5]]
輸出
4
更新於：2020年4月30日
1K+ 瀏覽量
廣告