資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學C++ 中帶括號的二叉樹轉字串
在這個問題中，我們給定一個二叉樹。我們的任務是建立一個程式，將二叉樹轉換為 C++ 中帶括號的字串。
二叉樹的值是整數，並將以先序遍歷的方式提供給程式。字串應該只包含整數和括號 ()，並且應該是最佳化的，即所有空括號對都應被消除。
**二叉樹**是一種樹，其特殊條件是每個節點最多可以有兩個子節點。
二叉樹示例：
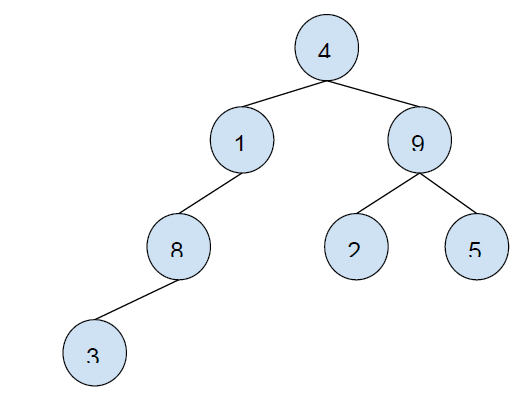
先序遍歷：[4, 1, 8, 3, 9, 2, 5]
**讓我們舉個例子來理解這個問題**
輸入
preorder: [4, 1, 8, 3, 9, 2, 5]
輸出
解釋
Root -> 4()() -> 4(1()())(9) -> 4(1(8()())())(9) -> 4(1(8(3)())())(9) -> 4(1(8(3)())())(9(2)(5))
消除所有空括號：
4(1(8(3)))(9(2)(5))
現在，讓我們解決這個問題，我們將進行二叉樹的先序遍歷，並在必要時放置括號。此外，我們必須消除額外的括號對。為此，我們將使用遞迴呼叫一個函式來放置括號。
我們將列印一個節點，併為該節點的兩個子節點遞迴呼叫該函式，直到該節點沒有子節點（即葉子節點）。
在為節點的子節點呼叫函式時，我們將遇到以下四種情況之一：
**情況 1** - 當節點同時具有左子節點和右子節點時。我們將為兩個子節點都放置括號，並將它們的值放在括號內，如果還有子節點，則呼叫它們的子節點。
示例 - 從上面的例子中，對於根節點 4，其中左右子節點都存在，4(1)(9)。
**情況 2** - 當節點只有左子節點時。我們將左子節點放入括號中，因為沒有右子節點，所以它的括號將被消除。並且只調用左子節點的子樹（如果有）。
示例 - 從上面的例子中，對於值為 1 的節點，只有左子節點存在，4(1(8()()))(9)。
**情況 3** - 當節點只有右子節點時。我們將為左子節點放置一個空括號。並將右子節點的值放置進去，如果還有子樹，則呼叫它的子樹。
**情況 4** - 當節點沒有子節點（葉子節點）時。我們不會放置任何括號，只放置值。
**示例** - 從上面的例子中，對於值為 5 的節點，沒有子節點，4(1(8(3)))(9(2)(5()()))。
將二叉樹轉換為帶括號的字串的程式
// 將二叉樹轉換為帶括號的字串的程式
示例
#include <iostream>
using namespace std;
struct Node {
int data;
Node *left, *right;
};
Node* insertNode(int data){
Node* node = (Node*)malloc(sizeof(Node));
node->data = data;
node->left = node->right = NULL;
return (node);
}
void ConveryBinaryTreeToString(Node* root, string& str){
if (root == NULL)
return;
str.push_back(root->data + '0');
if (!root->left && !root->right)
return;
str.push_back('(');
ConveryBinaryTreeToString(root->left, str);
str.push_back(')');
if (root->right) {
str.push_back('(');
ConveryBinaryTreeToString(root->right, str);
str.push_back(')');
}
}
int main() {
struct Node* root = insertNode(4);
root->left = insertNode(1);
root->right = insertNode(9);
root->left->left = insertNode(8);
root->left->left->left = insertNode(3);
root->right->left = insertNode(2);
root->right->right = insertNode(5);
string binaryTreeString = "";
ConveryBinaryTreeToString(root, binaryTreeString);
cout<<"The string with preorder traversal of binary tree with brackets is: "<<binaryTreeString;
}輸出
The string with preorder traversal of binary tree with brackets is: 4(1(8(3)))(9(2)(5))
400 次瀏覽
