資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究交流和電壓的平均值和有效值
交流量的平均值
交流量在一個週期內所有瞬時值的算術平均值稱為“交流量的平均值”。
$$平均值=\frac{一個週期內所有瞬時值的和}{瞬時值的個數}$$
$$=\frac{時間週期T內曲線下的總面積}{時間週期(T)} $$
$$=\frac{i_{1}+i_{2}+i_{3}+...+i_{n}}{n}$$
對稱波形的平均值
對於像正弦電壓或電流這樣的對稱波形，在一個週期內的平均值為零。這是因為正半週期與負半週期完全相等。但正半週期或負半週期的平均值不為零。因此，對於對稱波形，平均值是在半個週期內計算的。
$$平均值 = \frac{半個週期內所有瞬時值的和}{半個週期內瞬時值的個數}$$
非對稱波形的平均值
對於像半波整流電壓這樣的非對稱波形，平均值是在整個週期內計算的。
$$平均值 = \frac{半個週期內所有瞬時值的和}{一個週期內瞬時值的個數}$$
由於正弦交流電壓和電流在全世界範圍內得到了最廣泛的應用。因此，我們找到正弦電壓和電流的平均值和有效值。
正弦電壓或電流的平均值
交流（正弦電壓或電流）的平均值是直流的值，該值在半個週期內透過電路傳送的電荷量與交流在相同時間內透過相同電路傳送的電荷量相同。它用 Iav 表示。
正弦交流電壓或電流在一個週期內的平均值為零。這是因為正半週期的面積與負半週期的面積完全相等。但是，在半個週期（正或負）內的平均值不為零。因此，正弦電壓或電流的平均值是指半個週期的平均值。
推導 – 交流的平均值可以透過將電流或電壓的瞬時值在半個週期內積分（即半個週期內曲線的面積）並將結果除以半個週期的基長來獲得。
$$平均值=\frac{半個週期內的面積}{半個週期的基長}$$
正弦變化電壓的方程由下式給出
$$
u=V_{m}\sin\theta$$
讓我們在波形的正半週期內取一個厚度為 dθ 的條帶。考慮 v 為條帶的平均高度。因此，
$$條帶的面積=
u\:d\theta$$
$$半個週期的面積=\int_{0}^{\pi}
u\:\sin\theta\:d\theta$$
$$=V_{m}[-\cos\theta]_0^\pi=2V_{m}$$
$$平均值(V_{a
u})=\frac{半個週期的面積}{半個週期的基長}=\frac{2V_{m}}{\pi}=0.637V_{m}$$
類似地，對於正弦交流電流，
$$平均值(I_{a
u})=\frac{半個週期的面積}{半個週期的基長}=\frac{2l_{m}}{\pi}=0.637l_{m}$$
因此，正弦交流電流或電壓的平均值等於最大值或峰值的 0.637 倍。
正弦電壓或電流的有效值
正弦交流電流（AC）的均方根 (RMS) 或有效值是直流的值，當其在給定時間內流過給定電阻時，產生的熱量與交流在相同時間內流過相同電阻時產生的熱量相同。
有效值 = 電流的平方均值的平方根
$$交流電流的有效值(𝐼) =\sqrt{i^{2}的平均值}=\sqrt{\frac{i_{1}^{2}+i_{2}^{2}+i_{3}^{2}+...+i_{n}^{2}}{n}}$$
類似地，交流電壓的有效值可以表示為 -
$$交流電壓的有效值(
u) =\sqrt{
u^{2}的平均值}=\sqrt{\frac{
u_{1}^{2}+
u_{2}^{2}+
u_{3}^{2}+...+
u_{n}^{2}}{n}}$$
對於對稱波形，有效值可以透過考慮半個週期或整個週期來計算。但是，對於非對稱波形，應考慮整個週期。
對於對稱波，
$$有效值=\sqrt{\frac{半個週期平方波的面積}{半個週期的基長}}$$
正弦電流或電壓的有效值
由於正弦波是對稱波。因此，我們可以透過僅考慮半個週期來計算其有效值。
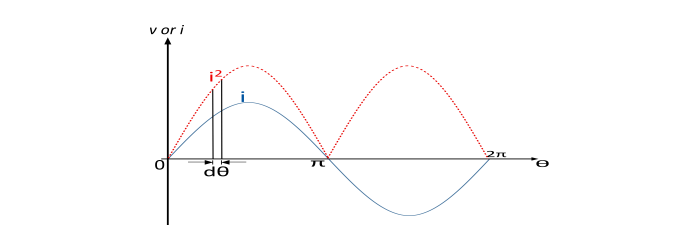
正弦交流電流的方程由下式給出
$$i=I_{m}\sin\theta$$
讓我們考慮在平方電流波（顯示為紅色虛線）的正半週期內取一個寬度為 dθ 的條帶。設 i2 為條帶的平均高度。
$$條帶的面積=i^{2}\:d\theta$$
$$平方波半個週期的面積=\int_{0}^{\pi}i^{2}\:d\theta=\int_{0}^{\pi}I_{m}^{2}\sin^{2}\theta\:d\theta$$
$$=I_{m}^{2}\int_{0}^{\pi}\sin^{2}\theta\:d\theta=\frac{\pi\:I^{2}m}{2}$$
因此，
$$I_{RMS}=\sqrt{\frac{平方波半個週期的面積}{半個週期的基長}}=\sqrt{\frac{{\pi\:I_{m}^{2}}/{2}}{\pi}}=\frac{I_{m}}{\sqrt{2}}=0.707I_{m}$$
類似地，正弦交流電壓的有效值為
$$V_{RMS}=\frac{V_{m}}{\sqrt{2}}=0.707V_{m}$$
因此，正弦交流電壓或電流的有效值等於峰值的 0.707 倍。
數值示例 #1
一個正弦電流的最大值為 650 mA。它的平均值是多少？
解決方案
正弦交流電流的平均值由下式給出
$$I_{a
u}=\frac{2I_{m}}{\pi}=0.637I_{m}$$
$$I_{a
u}=0.637 × 650 ×\:10^{-3}=414.05mA$$
數值示例 #2
交流電壓的方程由 ν = 325.22 𝑠𝑖𝑛314𝑡 給出。求 (i) 有效值 (ii) 頻率 (iii) 平均值。
解決方案
電壓的最大值為
$$V_{m}=325.22 V$$
電壓的有效值
$$V_{RMS}=0.707𝑉𝑚 = 0.707 × 325.22 = 230 V$$
頻率
$$\because\:\omega= 2𝜋𝑓 = 31$$
$$\therefore\:f=\frac{\omega}{2\pi}=\frac{314}{2\pi}=50 Hz$$
平均值
$$V_{a
u}=0.637𝑉𝑚 = 0.637 × 325.22 = 207.2 V$$
36K+ 次檢視
