六邊形面積公式

---

簡介

六邊形的面積是由其所有邊圍成的空間。六邊形是一個具有六條邊和六個角的多邊形。正六邊形由六個等邊三角形組成，具有六條相等的邊和六個相等的角。計算六邊形面積的方法有很多，無論是形狀不規則的六邊形還是正六邊形。

計算六邊形面積公式的方法有很多。各種方法主要取決於你如何分割六邊形。它可以被分成6個等邊三角形或2個三角形和1個矩形。在本教程中，我們將討論六邊形面積公式。

六邊形

• 六邊形是由六條直線組成的封閉二維形狀。它在二維空間中具有六條邊、六個頂點和六個內角。

• 六邊形形狀的現實世界例子包括：六角形地磚、鉛筆橫截面、鐘錶、蜂窩等。它可以是正六邊形（六條邊長和角度相等）或不規則六邊形（6條邊長和角度不相等）。

• 正六邊形

  正六邊形是一個封閉的二維形狀，具有六條相等的邊和六個相等的角。每個正六邊形的角度為120度。

  所有內角的總和為 120 x 6 = 720 度。對於外角，我們知道任何多邊形的外角之和始終為 360°。六邊形有六個外角。

  因此，正六邊形的每個外角為 $\mathrm{\frac{360}{6} = 60}$ 度。

正六邊形與不規則六邊形的區別在於，不規則六邊形的角度和邊長沒有確定的測量值，並且邊長不同。不規則六邊形和正六邊形共有的某些屬性如下：

• 兩者都有六條邊、六個內角和六個頂點。

• 所有六個內角加起來等於 720 度。

• 所有六個外角加起來等於 360 度。

六邊形的面積

• 六邊形的面積是由六邊形的邊圍成的區域。

  正六邊形的面積為 $\mathrm{\frac{3\sqrt{3} s^2}{2}}$

  其中 s 是六邊形邊的長度。因為我們討論的是正六邊形，所以所有邊的長度都相同。

  當已知正六邊形的一條邊的長度時，可以使用以下公式計算面積：

• 已知旁心距的六邊形面積計算公式為：面積 = $\mathrm{\frac{1}{2} × 周長 × 旁心距}$。

透過將六邊形分成三角形來計算面積

邊邊邊規則確保六邊形內的所有三角形都全等；每個三角形有兩條邊在六邊形內部，以及構成六邊形周長的底邊。同樣，所有三角形的角度都相同。

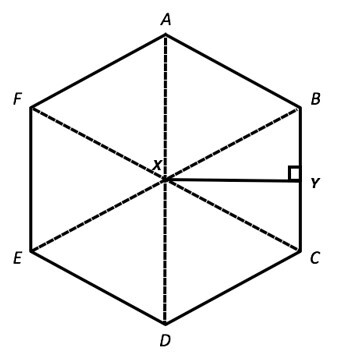
因此，六邊形的面積將表示為 ${\mathrm{6×\frac{\sqrt{3} s^2}{4}}}$

$$\mathrm{ =\frac{3\sqrt{3} s^2}{2}}$$

正六邊形的面積為 $\mathrm{ \frac{3\sqrt{3} s^2}{2}}$，其中 s 是六邊形邊的長度。

例題

1) 如果每條邊的長度為 4，則求六邊形的面積。

答案：已知每條邊的長度為 4，我們知道正六邊形的面積為 $\mathrm{ \frac{3\sqrt{3} s^2}{2}}$，其中 s 是六邊形邊的長度。

正六邊形的面積=$\mathrm{ \frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{ \frac{3\sqrt{3} \times 4^2}{2}}$$

$$\mathrm{=24\sqrt{3}}$$

2) 如果每條邊的長度為 2，則求六邊形的面積。

答案：已知每條邊的長度為 2，我們知道正六邊形的面積為 $\mathrm{ \frac{3\sqrt{3} s^2}{2}}$，其中 s 是六邊形邊的長度。

正六邊形的面積=$\mathrm{ \frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{ \frac{3\sqrt{3} \times 2^2}{2}}$$

$$\mathrm{=6\sqrt{3}}$$

3) 如果六邊形的周長為 24，旁心距為 3，則求六邊形的面積。

我們知道已知旁心距的六邊形面積計算公式。簡而言之，

$$\mathrm{面積 =\frac{1}{2} × 24 ×3.}$$

$$\mathrm{=36}$$

4) 如果六邊形的周長為 4，旁心距為 1，則求六邊形的面積。

答案：已知周長為 4，旁心距為 1。

我們知道已知旁心距的六邊形面積計算公式。簡而言之，

$$\mathrm{面積 =\frac{1}{2}× 周長 ×旁心距.}$$

$$\mathrm{面積 =\frac{1}{2}× 4 ×1.}$$

$$\mathrm{=2}$$

5) 如果六邊形的面積為 20，旁心距為 4，則求六邊形的周長。

答案：已知六邊形的面積為 20，旁心距為 4。

現在使用關係式，$\mathrm{面積 =\frac{1}{2}× 周長 ×旁心距.}$

$$\mathrm{20 =\frac{1}{2}\times 周長 \times 4}$$

$$\mathrm{\Rightarrow 周長=10}$$

6) 如果六邊形的面積為 100，旁心距為 8，則求六邊形的周長。

答案：已知六邊形的面積為 100，旁心距為 8。

現在使用關係式，$\mathrm{面積 =\frac{1}{2}× 周長 ×旁心距.}$

$$\mathrm{100 =\frac{1}{2}× 周長 ×8.}$$

$$\mathrm{\Rightarrow 周長=25}$$

7) 如果已知面積為 6√3，則求正六邊形的邊長。

答案：已知六邊形的面積為 6√3。

現在使用正六邊形面積關係式=$\mathrm{\frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{s=2}$$

8) 如果已知面積為 3√3，則求正六邊形的邊長。

答案：已知六邊形的面積為 3√3。

現在使用正六邊形面積關係式=$\mathrm{\frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{3\sqrt{3}=\frac{3\sqrt{3} s^2}{2}}$$

$$\mathrm{s=\sqrt{2}}$$

結論

六邊形是一個六邊多邊形，有六個角。它源於希臘詞“Hexa”（六）和“gon”（角）。

正六邊形的面積為 $\mathrm{\frac{3\sqrt{3} s^2}{2}}$，其中 s 是六邊形邊的長度。

常見問題

1. 六邊形是什麼意思？

六邊形是由六條直線組成的封閉二維形狀。它在二維空間中具有六條邊、六個頂點和六個內角。

2. 求六邊形面積的公式是什麼？

求六邊形面積的公式是 $\mathrm{\frac{3\sqrt{3} s^2}{2}}$。

3. 六邊形的角度是多少？

六邊形所有六個內角之和為 720 度。正六邊形的每個內角為 120 度。

4. 正六邊形到底是什麼？

正六邊形是一種六邊形，其所有邊都相等。此外，正六邊形的所有六個角都相等。

5. 不規則六邊形到底是什麼？

與其他邊和角相比，不規則六邊形至少有一條邊和一個角不相等。每個角沒有確定的測量值，但所有六個內角之和始終為 720 度，所有六個外角之和為 360 度。

6. 正六邊形有多少條對稱線？

所有正多邊形的對稱線數量等於邊的數量。因此，正六邊形有六條對稱線。