正六邊形

---

引言

如果一個多邊形具有相等的二維封閉形狀，並且所有多邊形的邊和內角都相等，則它們被稱為正多邊形。正方形和等邊三角形是正多邊形的一些例子。正六邊形是一個封閉形狀的多邊形，它有六條相等的邊和六個相等的角。在本教程中，我們將學習正六邊形、正六邊形的角、正六邊形的外部角、正六邊形的對角線和對稱線、六邊形平鋪、現實生活中的六邊形以及一些相關的已解決示例。

正六邊形

“六邊形”一詞，“hex”意為六，“gonia”意為角，六邊形可以定義為二維幾何中的六邊形。正六邊形是一個六邊形，它具有六條等長的邊和相等的內角。正六邊形由六個等邊三角形組成。正六邊形是一個二維圖形，它有六條邊、六個內角和六個頂點。蜂窩、地板磚和鐘錶是正六邊形的一些例子。

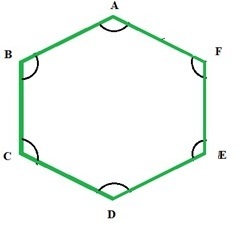
六邊形的角

六邊形有兩種型別的角：內角和外角。正六邊形有六個內角和六個外角。正六邊形所有內角的和為 720°，所有外角的和為 360°。

由於正多邊形的角都相等，因此正六邊形的每個角都可以透過 720° ÷ 6 = 120° 計算得出。類似地，正六邊形的外部角可以透過 360° ÷ 6 = 60° 計算得出。

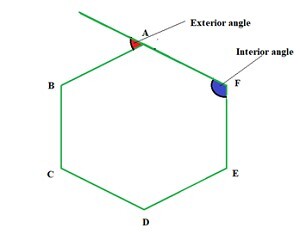
六邊形的外角

如圖所示，如果正六邊形的一條邊延伸，它與六邊形的相鄰邊構成一個角，這樣的角稱為六邊形的外角。

正六邊形的外角計算方法為：

外角 = 所有外角之和 / 6。

= 360°/6

= 60°

因此，正六邊形的外角為 60°。

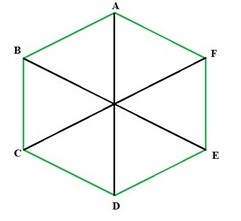
六邊形對角線的數量

對角線是在封閉形狀圖形上連線彼此相對頂點的線。正六邊形的對角線也可以類似地繪製。正六邊形有九條對角線，對應六個頂點。當繪製所有對角線時，它們將正六邊形分成六個等邊三角形。如圖所示，對角線在中心形成 60 度角。

多邊形的對角線數量可以透過公式 n(n-3)/2 計算。

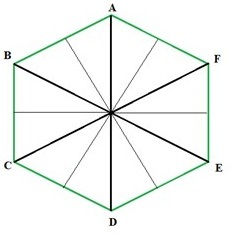
六邊形的對稱線

對稱線可以定義為穿過圖形中心並將圖形分成兩個相同部分的線。如圖所示，當為正六邊形繪製對稱線時，得到六條對稱線。

正六邊形週期性地平鋪平面

歐幾里得平面的六邊形平鋪可以定義為一個正平鋪，其中一個頂點由三個六邊形共享。我們可以透過將 360 除以多邊形的內角（在本例中為 120 度）來確定這一點。歐幾里得平面的正平鋪可以透過三種方式完成，即透過等邊三角形、正方形和正六邊形。六邊形平鋪具有 6 重對稱性，即六邊形平鋪可以旋轉 60^o 6 次，並且平鋪始終看起來與原始平鋪相似。六邊形平鋪，也稱為六邊形鑲嵌，由著名數學家約翰·康威命名為六邊形。

現實生活中的六邊形

我們可以在自然界和人工結構中看到六邊形圖案。當我們平鋪平面時，六邊形結構彼此契合，沒有任何縫隙。因此，蜂窩的細胞是六邊形的，因為六邊形形狀可以有效地利用空間。在化合物的結構中，石墨烯具有六邊形網狀晶體結構。另一個化合物的例子是苯，它是一種具有六邊形分子結構的碳化合物，被認為是化學中最強的結構之一。六邊形形狀也已用於宇宙學，例如詹姆斯·韋伯太空望遠鏡，它具有 18 個六邊形鏡面段，以捕捉儘可能多的光線來觀察宇宙中遙遠的恆星。

已解決的示例

1.如果正六邊形的一條邊長為 6 個單位，則計算其面積。

解答

我們知道：

正六邊形的面積由 $\mathrm{\frac{3\sqrt{3} s^2}{2}}$ 平方單位給出，其中 s 表示邊的單位長度。

已知，邊 s = 6 個單位。

因此，面積 $\mathrm{A=\frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{A=\frac{3\sqrt{3} 6^2}{2}}$$

= 54√3 平方單位。

因此，正六邊形的面積為 54√3 平方單位。

2.如果正六邊形的面積為 72√3 平方單位，則求其每條邊的長度。

解答

正六邊形的面積由 $\mathrm{\frac{3\sqrt{3} s^2}{2}}$ 平方單位給出，其中 s 表示邊的單位長度。

因此，$\mathrm{72\sqrt{3}=\frac{3\sqrt{3} s^2}{2}}$

$$\mathrm{72=\frac{3}{2} s^2}$$

72×2 = 3s²

48 = s²

s = 4√3

因此，六邊形的邊長為 4√3。

結論

如果一個多邊形具有相等的二維封閉形狀，並且所有多邊形的邊和內角都相等，則它們被稱為正多邊形。正六邊形是一個封閉形狀的多邊形，它有六條相等的邊和六個相等的角。“六邊形”一詞，“hex”意為六，“gonia”意為角。正多邊形有六個內角和六個外角。正六邊形所有內角的和為 720 度，所有外角的和為 360 度。每個正六邊形有九條對角線。當為正六邊形繪製對稱線時，得到六條對稱線。

常見問題

1. 正六邊形的周長是多少？

正六邊形的周長可以透過將正六邊形的邊長乘以 6 來計算。

2. 定義正六邊形的內角和外角。

正六邊形的內角為 120 度，外角為 60 度。

3. 正六邊形的現實生活中的例子是什麼？

在雪花顯微照片以及蜂窩結構中可以看到正六邊形。

4. 六邊形與等邊三角形有什麼關係？

正六邊形由六個等邊三角形組成，可以透過連線正六邊形的對角線來繪製。

5. 正多邊形有多少條對稱線？

正六邊形有 6 條對稱線。