資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究已知半徑，求n邊正多邊形的面積？
我們將學習如何計算已知半徑的n邊正多邊形的面積。這裡的半徑是指從中心到任何一個頂點的距離。為了解決這個問題，我們從中心向一邊作垂線。設每條邊的長度為'a'。垂線將邊分成兩部分，每部分的長度為a/2。垂線和一條半徑構成一個角度x。設半徑的長度為h。
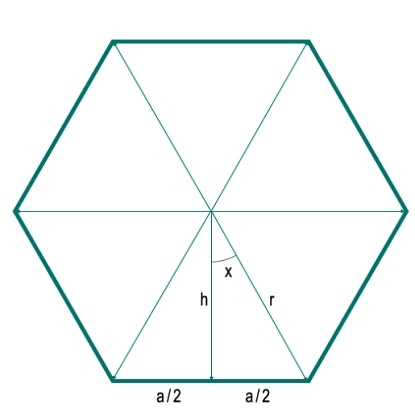
我們可以看到，多邊形被分成N個相等的三角形。因此，任何N邊多邊形都被分成N個三角形。所以中心角為360°，被分成360°/N個不同的角（這裡360°/6 = 60°）。所以角度x為180°/N。現在我們可以很容易地使用三角方程得到h和a。
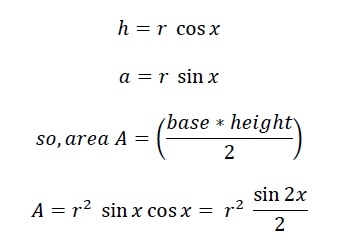
現在整個多邊形的面積是N*A。
示例
#include <iostream>
#include <cmath>
using namespace std;
float polygonArea(float r, int n){
return ((r * r * n) * sin((360 / n) * 3.1415 / 180)) / 2; //convert
angle to rad then calculate
}
int main() {
float rad = 9.0f;
int sides = 6;
cout << "Polygon Area: " << polygonArea(rad, sides);
}輸出
Polygon Area: 210.44
更新於：2019年8月1日
219 次瀏覽
廣告