資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學C/C++ 中的 2-3 樹（搜尋和插入）？
2-3 樹定義為一種樹形資料結構，其中每個具有子節點的內部節點要麼有兩個子節點（2-節點）和一個數據元素，要麼有三個子節點（3-節點）和兩個資料元素。
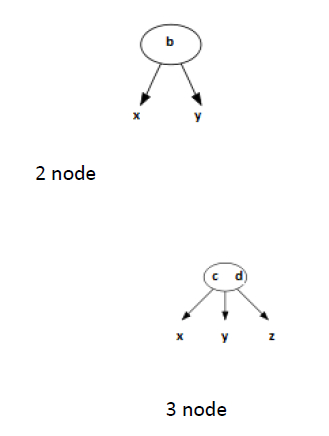
定義
如果一個內部節點具有一個數據元素和兩個子節點，則稱其為 2-節點。
如果一個內部節點具有兩個資料元素和三個子節點，則稱其為 3-節點。
當且僅當以下語句之一滿足時，我們稱 T 為 2-3 樹：
T 為空。換句話說，T 不包含任何節點。
T 是一個具有資料元素 a 的 2-節點。如果 T 具有左子節點 L 和右子節點 R，則我們得出結論：
L 和 R 被視為相同高度的非空 2-3 樹；
a 大於 L 中的每個元素；並且
a 小於或等於 R 中的每個資料元素。
T 是一個具有資料元素 a 和 b 的 3-節點，其中 a 小於 b。如果 T 具有左子節點 L、中間子節點 M 和右子節點 R，則我們得出結論：
L、M 和 R 被視為相同高度的非空 2-3 樹；
a 大於 L 中的每個資料元素且小於或等於 M 中的每個資料元素；並且
b 大於 M 中的每個資料元素且小於或等於 R 中的每個資料元素。
屬性
每個內部節點都被視為 2-節點或 3-節點。
所有葉子節點都位於同一層。
所有資料都保持排序。
操作
搜尋
在 2-3 樹中搜索專案與在二叉搜尋樹中搜索專案相同。由於每個節點中的資料元素都是有序的，因此搜尋函式將被引導到正確的子樹，最終到達包含該專案的正確節點。
設 T 為 2-3 樹，d 為我們要查詢的資料元素。如果 T 為空，則 d 不在 T 中，我們完成操作。
設 r 為 T 的根節點。
設 r 為葉子節點。如果 d 不在 r 中，則 d 不在 T 中。否則，d 在 T 中。特別是，d 可以在葉子節點中找到。我們不需要進一步步驟，操作完成。
假設 r 是一個具有左子節點 L 和右子節點 R 的 2-節點。設 e 為 r 中的資料元素。
有三種情況：
如果 d 等於 e，則我們在 T 中找到 d，操作完成。
如果 d 小於 e，則將 T 設定為 L（根據定義，L 是一個 2-3 樹），並返回步驟 2。
如果 d 大於 e，則將 T 設定為 R，並返回步驟 2。
假設 r 是一個具有左子節點 L、中間子節點 M 和右子節點 R 的 3-節點。設 a 和 b 為 r 的兩個資料元素，其中 a
如果 d 等於 a 或 b，則 d 在 T 中，操作完成。
如果 d 小於 a，則將 T 設定為 L，並返回步驟 2。
如果 a 小於 d 且 d 小於 b，則將 T 設定為 M，並返回步驟 2。
如果 d 大於 b，則將 T 設定為 R，並返回步驟 2。
插入
插入透過搜尋鍵的正確位置並將其新增到該位置來執行。如果節點變成 4-節點，則該節點將被分成兩個 2-節點，中間鍵將被移動到父節點。然後父節點可能會變成 4-節點，在這種情況下，它也會被分割，並將鍵傳播到其父節點。此過程重複進行，直到我們到達不需要分割的 2-節點父節點，或者到達根節點，在這種情況下，我們將傳播的元素實現為建立一個新的 2-節點根節點。藉助此演算法，執行的運算元量與樹的高度成正比，因此由於樹是完全平衡的，所以是對數級的。此過程確保其結果為 2-3 樹：特別是，所有葉子節點都保持在相同的深度。
下圖解釋了此過程的可能情況。
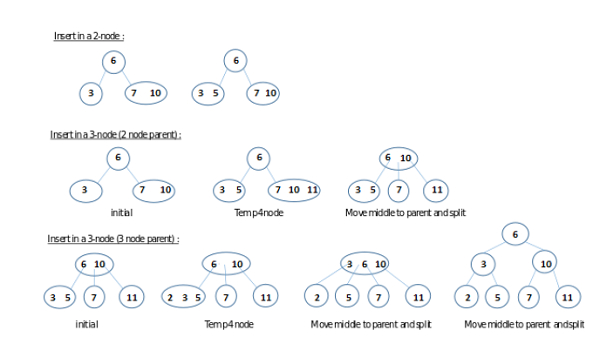
在 2-3 樹中插入數字的 3 種可能情況。
668 次瀏覽
