資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
時尚研究
法律研究資料結構中的最優二叉搜尋樹
給定一組已排序的整數和一個表示頻率的陣列 freq。我們的任務是用這些資料建立一個二叉搜尋樹，以查詢所有搜尋的最小開銷。
建立了一個輔助陣列 cost[n, n] 來求解和儲存子問題的解答。開銷矩陣將包含資料，以自下而上的方式解決問題。
輸入 − 關鍵字作為節點及頻率。
Keys = {10, 12, 20}
Frequency = {34, 8, 50}輸出 − 最小開銷是 142。
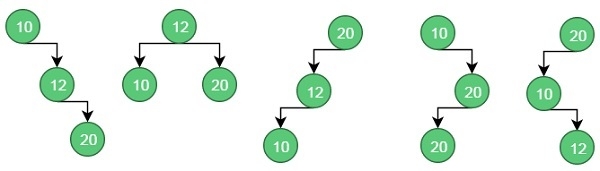
以下是給定值可能出現的二叉搜尋樹。
對於情況 1，開銷為：(34*1) + (8*2) + (50*3) = 200
對於情況 2，開銷為：(8*1) + (34*2) + (50*2) = 176。
類似地，對於情況 5，開銷為：(50*1) + (34 * 2) + (8 * 3) = 142（最小）
演算法
optCostBst(keys, freq, n) Input: Keys to insert in BST, frequency for each keys, number of keys. Output: Minimum cost to make optimal BST. Begin define cost matrix of size n x n for i in range 0 to n-1, do cost[i, i] := freq[i] done for length in range 2 to n, do for i in range 0 to (n-length+1), do j := i + length – 1 cost[i, j] := ∞ for r in range i to j, done if r > i, then c := cost[i, r-1] else c := 0 if r < j, then c := c + cost[r+1, j] c := c + sum of frequency from i to j if c < cost[i, j], then cost[i, j] := c done done done return cost[0, n-1] End
示例
#include <iostream>
using namespace std;
int sum(int freq[], int low, int high){ //sum of frequency from low to high range
int sum = 0;
for (int k = low; k <=high; k++)
sum += freq[k];
return sum;
}
int minCostBST(int keys[], int freq[], int n){
int cost[n][n];
for (int i = 0; i < n; i++) //when only one key, move along diagonal elements
cost[i][i] = freq[i];
for (int length=2; length<=n; length++){
for (int i=0; i<=n-length+1; i++){ //from 0th row to n-length+1 row as i
int j = i+length-1;
cost[i][j] = INT_MAX; //initially store to infinity
for (int r=i; r<=j; r++){
//find cost when r is root of subtree
int c = ((r > i)?cost[i][r-1]:0)+((r < j)?cost[r+1][j]:0)+sum(freq, i, j);
if (c < cost[i][j])
cost[i][j] = c;
}
}
}
return cost[0][n-1];
}
int main(){
int keys[] = {10, 12, 20};
int freq[] = {34, 8, 50};
int n = 3;
cout << "Cost of Optimal BST is: "<< minCostBST(keys, freq, n);
}輸出
Cost of Optimal BST is: 142
更新於：2019 年 8 月 27 日
已觀看 1 千次
廣告