資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
Microsoft Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學2-3 樹 - C++ 資料結構與演算法
2-3 樹是一種資料結構中的樹，其中樹的每個節點要麼是 2 節點
要麼是 3 節點。它是階數為 3 的特殊型別的B 樹。
樹中的 2 節點是一個具有一個數據部分和兩個子節點的節點。
樹中的 3 節點是一個具有兩個資料部分和三個子節點的節點。
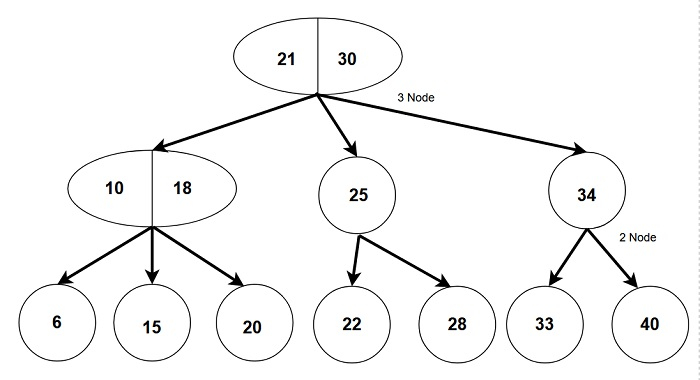
圖：2-3 樹
2-3 樹的特性：
每個內部節點要麼是 2 節點，要麼是 3 節點。
包含一個數據部分的節點可以是具有恰好 2 個子節點的 2 節點，也可以是沒有任何子節點的葉節點。
包含兩個資料部分的節點只能是具有恰好 3 個子節點的 3 節點。
所有葉節點始終處於同一級別。
2-3 樹始終是高度平衡的樹。
在 2-3 樹中，搜尋操作快速有效。
2 節點：
正好有兩個子節點。
左子節點權重較小。
右子節點權重較大。
可以是沒有任何子節點的葉節點。
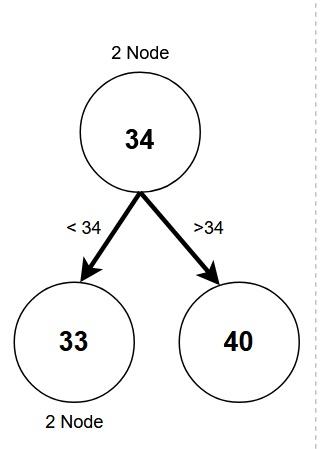
3 節點：
正好有三個子節點。
2 個數據值。
左子節點權重小於左資料值。
中間子節點權重介於兩個資料值之間。
右子節點權重大於右資料值。
永遠不能是葉節點。
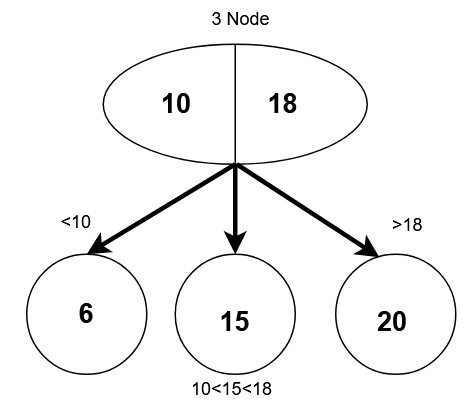
2-3 樹中的操作：
1. 在 2-3 樹中搜索
與二叉搜尋樹中的搜尋操作類似，因為資料已排序。
在 2-3 樹中搜索 X。
如果樹為空 → 返回 False
如果到達根節點，則返回 False（未找到）
如果 X 小於左資料部分，則搜尋左子樹
如果 X 大於左資料且大於右資料，則搜尋中間子樹。
如果 X 大於右資料部分，則搜尋右子樹。
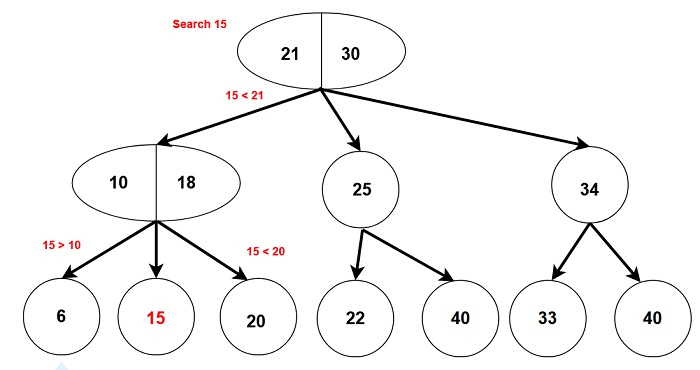
2. 在 2-3 樹中插入節點
在 2-3 樹中插入 X。
如果樹為空 → 將 X 作為根新增。
搜尋 X 的正確位置並將其新增為葉節點。
如果葉節點只有一個數據部分，則新增 X，葉節點變為 2 節點。
如果葉節點有兩個資料部分，則新增 X。拆分臨時 3 節點並將資料根據排序順序移動到父節點。
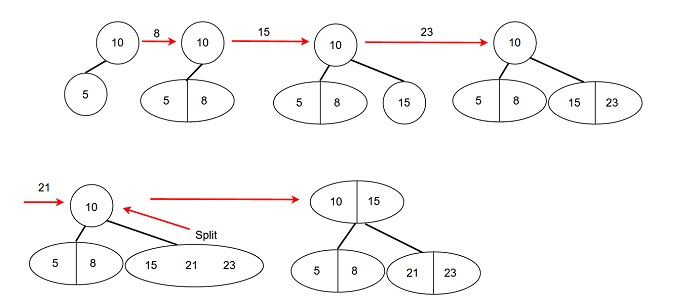
建立 2-3 樹並按順序新增節點 → 10, 5, 8, 15, 23, 21
3. 從 2-3 樹中刪除節點
從 2-3 樹中刪除 X。
如果樹為空，則返回 false。
搜尋 X 的位置並將其刪除，然後調整樹。
如果 X 是 3 節點的一部分，則刪除 X 並調整左值和中間值。如有必要，還要調整節點祖先的左值和中間值。
如果 X 是 2 節點的一部分，則以遞迴方式調整和拆分樹，並按排序順序排列節點。
6000+ 次瀏覽
