
Theano - 快速指南
Theano - 簡介
您是否使用 Python 開發過機器學習模型?那麼,您顯然知道開發這些模型的複雜性。開發過程通常是一個緩慢的過程,需要花費數小時甚至數天的時間進行計算。
機器學習模型的開發需要大量的數學計算。這些通常需要算術運算,尤其是多維的大型矩陣。如今,我們使用神經網路而不是傳統的統計技術來開發機器學習應用程式。神經網路需要在海量資料上進行訓練。訓練是分批進行的,每批資料的大小合理。因此,學習過程是迭代的。因此,如果計算效率不高,訓練網路可能需要數小時甚至數天。因此,高度期望最佳化可執行程式碼。而這正是 Theano 提供的。
Theano 是一個 Python 庫,它允許您定義機器學習中使用的數學表示式,最佳化這些表示式並在關鍵區域果斷地使用 GPU 來非常有效地評估這些表示式。在大多數情況下,它可以與典型的完整 C 實現相媲美。
Theano 在 LISA 實驗室編寫,旨在快速開發高效的機器學習演算法。它是在 BSD 許可下發布的。
在本教程中,您將學習如何使用 Theano 庫。
Theano - 安裝
Theano 可以安裝在 Windows、MacOS 和 Linux 上。在所有情況下,安裝都非常簡單。在安裝 Theano 之前,您必須安裝其依賴項。以下是依賴項列表:
- Python
- NumPy - 必需
- SciPy - 僅當需要稀疏矩陣和特殊函式時才需要
- BLAS - 提供執行基本向量和矩陣運算的標準構建塊
您可以根據需要選擇安裝的可選軟體包為:
- nose:執行 Theano 的測試套件
- Sphinx - 用於構建文件
- Graphiz 和 pydot - 用於處理圖形和影像
- NVIDIA CUDA 驅動程式 - GPU 程式碼生成/執行所需
- libgpuarray - 在 CUDA 和 OpenCL 裝置上進行 GPU/CPU 程式碼生成所需
我們將討論在 MacOS 上安裝 Theano 的步驟。
MacOS 安裝
要安裝 Theano 及其依賴項,請使用以下命令列中的 **pip**。這些是在本教程中我們將需要的最小依賴項。
$ pip install Theano $ pip install numpy $ pip install scipy $ pip install pydot
您還需要使用以下命令安裝 OSx 命令列開發者工具:
$ xcode-select --install
您將看到以下螢幕。點選 **安裝** 按鈕安裝工具。

安裝成功後,您將在控制檯上看到成功訊息。
測試安裝
安裝成功完成後,在 Anaconda Jupyter 中開啟一個新的筆記本。在程式碼單元格中,輸入以下 Python 指令碼:
示例
import theano from theano import tensor a = tensor.dscalar() b = tensor.dscalar() c = a + b f = theano.function([a,b], c) d = f(1.5, 2.5) print (d)
輸出
執行指令碼,您應該會看到以下輸出:
4.0
為了方便您快速參考,下面顯示了執行的螢幕截圖:
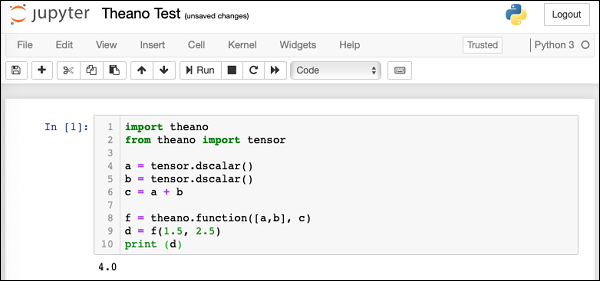
如果您獲得上述輸出,則您的 Theano 安裝成功。否則,請按照 Theano 下載頁面上的除錯說明解決問題。
什麼是 Theano?
既然您已成功安裝 Theano,讓我們首先嚐試瞭解什麼是 Theano?Theano 是一個 Python 庫。它允許您定義、最佳化和評估數學表示式,尤其是機器學習模型開發中使用的那些表示式。Theano 本身不包含任何預定義的 ML 模型;它只是促進了它的開發。在處理多維陣列時,它特別有用。它與 NumPy 無縫整合,NumPy 是 Python 中用於科學計算的基本且廣泛使用的軟體包。
Theano 促進了 ML 開發中使用的數學表示式的定義。此類表示式通常涉及矩陣算術、微分、梯度計算等。
Theano 首先為您的模型構建整個計算圖。然後,它透過對圖應用多種最佳化技術將其編譯成高效的程式碼。編譯後的程式碼透過 Theano 中稱為 **function** 的特殊操作注入到 Theano 執行時。我們重複執行此 **function** 來訓練神經網路。與使用純 Python 編碼甚至完整的 C 實現相比,訓練時間大大減少。
我們現在將瞭解 Theano 開發的過程。讓我們從如何在 Theano 中定義數學表示式開始。
Theano - 一個簡單的 Theano 表示式
讓我們從在 Theano 中定義和評估一個簡單的表示式開始我們的 Theano 之旅。考慮以下將兩個標量相加的簡單表示式:
c = a + b
其中 **a**、**b** 是變數,**c** 是表示式的輸出。在 Theano 中,即使定義和評估這個簡單的表示式也很棘手。
讓我們瞭解評估上述表示式的步驟。
匯入 Theano
首先,我們需要在程式中匯入 Theano 庫,我們使用以下語句:
from theano import *
在上面的語句中,我們使用 * 包含 Theano 庫中的所有軟體包,而不是匯入各個軟體包。
宣告變數
接下來,我們將使用以下語句宣告一個名為 **a** 的變數:
a = tensor.dscalar()
**dscalar** 方法宣告一個十進位制標量變數。執行上述語句將在您的程式程式碼中建立一個名為 **a** 的變數。同樣,我們將使用以下語句建立變數 **b**:
b = tensor.dscalar()
定義表示式
接下來,我們將定義對這兩個變數 **a** 和 **b** 進行操作的表示式。
c = a + b
在 Theano 中,執行上述語句不會執行這兩個變數 **a** 和 **b** 的標量加法。
定義 Theano 函式
要評估上述表示式,我們需要在 Theano 中定義一個函式,如下所示:
f = theano.function([a,b], c)
函式 **function** 接受兩個引數,第一個引數是函式的輸入,第二個引數是函式的輸出。上述宣告指出第一個引數是包含兩個元素 **a** 和 **b** 的陣列型別。輸出是一個稱為 **c** 的標量單元。此函式將在我們以後的程式碼中使用變數名 **f** 進行引用。
呼叫 Theano 函式
對函式 f 的呼叫使用以下語句進行:
d = f(3.5, 5.5)
函式的輸入是一個包含兩個標量的陣列:**3.5** 和 **5.5**。執行的輸出分配給標量變數 **d**。要列印 **d** 的內容,我們將使用 **print** 語句:
print (d)
執行將導致 **d** 的值列印到控制檯,在本例中為 9.0。
完整程式清單
為了方便您快速參考,這裡給出了完整的程式清單:
from theano import * a = tensor.dscalar() b = tensor.dscalar() c = a + b f = theano.function([a,b], c) d = f(3.5, 5.5) print (d)
執行上述程式碼,您將看到輸出為 9.0。此處顯示了螢幕截圖:
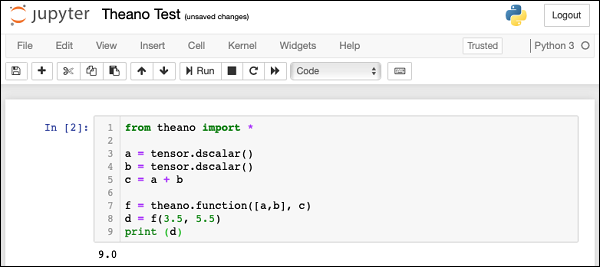
現在,讓我們討論一個稍微複雜一點的示例,該示例計算兩個矩陣的乘法。
Theano - 矩陣乘法的表示式
我們將計算兩個矩陣的點積。第一個矩陣的維度為 2 x 3,第二個矩陣的維度為 3 x 2。我們用作輸入的矩陣及其乘積在此處表示:
$$\begin{bmatrix}0 & -1 & 2\\4 & 11 & 2\end{bmatrix} \:\begin{bmatrix}3& -1 \\1 & 2 \\35 & 20 \end{bmatrix}=\begin{bmatrix}11 & 0 \\35 & 20 \end{bmatrix}$$宣告變數
要為上述內容編寫 Theano 表示式,我們首先宣告兩個變數來表示我們的矩陣,如下所示:
a = tensor.dmatrix() b = tensor.dmatrix()
dmatrix 是雙精度矩陣的型別。請注意,我們在任何地方都沒有指定矩陣大小。因此,這些變數可以表示任何維度的矩陣。
定義表示式
要計算點積,我們使用名為 **dot** 的內建函式,如下所示:
c = tensor.dot(a,b)
乘法的輸出分配給一個名為 **c** 的矩陣變數。
定義 Theano 函式
接下來,我們像前面的示例一樣定義一個函式來評估表示式。
f = theano.function([a,b], c)
請注意,函式的輸入是兩個變數 a 和 b,它們是矩陣型別。函式輸出分配給變數 **c**,該變數將自動為矩陣型別。
呼叫 Theano 函式
我們現在使用以下語句呼叫函式:
d = f([[0, -1, 2], [4, 11, 2]], [[3, -1],[1,2], [6,1]])
上述語句中的兩個變數是 NumPy 陣列。您可以像此處顯示的那樣顯式定義 NumPy 陣列:
f(numpy.array([[0, -1, 2], [4, 11, 2]]), numpy.array([[3, -1],[1,2], [6,1]]))
計算 **d** 後,我們列印其值:
print (d)
您將在輸出上看到以下輸出:
[[11. 0.] [25. 20.]]
完整程式清單
The complete program listing is given here: from theano import * a = tensor.dmatrix() b = tensor.dmatrix() c = tensor.dot(a,b) f = theano.function([a,b], c) d = f([[0, -1, 2],[4, 11, 2]], [[3, -1],[1,2],[6,1]]) print (d)
程式執行的螢幕截圖顯示在此處:
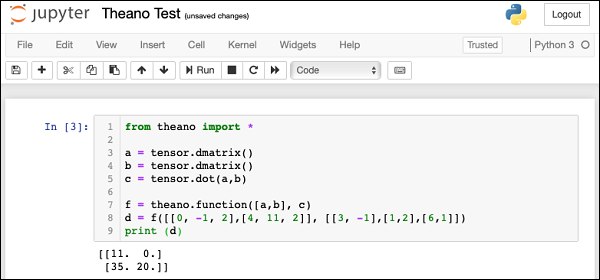
Theano - 計算圖
從以上兩個示例中,您可能已經注意到,在 Theano 中,我們建立了一個表示式,該表示式最終使用 Theano **function** 進行評估。Theano 使用高階最佳化技術來最佳化表示式的執行。為了視覺化計算圖,Theano 在其庫中提供了一個 **printing** 軟體包。
標量加法的符號圖
要檢視標量加法程式的計算圖,請使用以下方式使用 printing 庫:
theano.printing.pydotprint(f, outfile="scalar_addition.png", var_with_name_simple=True)
當您執行此語句時,將在您的機器上建立一個名為 **scalar_addition.png** 的檔案。此處顯示了儲存的計算圖,以供您快速參考:
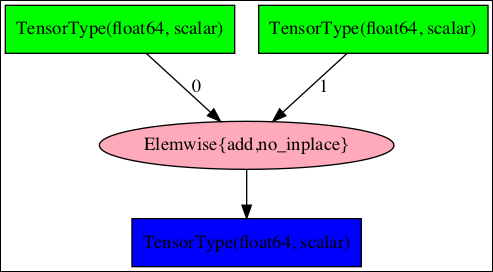
生成上述影像的完整程式清單如下所示:
from theano import * a = tensor.dscalar() b = tensor.dscalar() c = a + b f = theano.function([a,b], c) theano.printing.pydotprint(f, outfile="scalar_addition.png", var_with_name_simple=True)
矩陣乘法的符號圖
現在,嘗試為我們的矩陣乘法器建立計算圖。生成此圖的完整清單如下所示:
from theano import * a = tensor.dmatrix() b = tensor.dmatrix() c = tensor.dot(a,b) f = theano.function([a,b], c) theano.printing.pydotprint(f, outfile="matrix_dot_product.png", var_with_name_simple=True)
生成的圖顯示在此處:
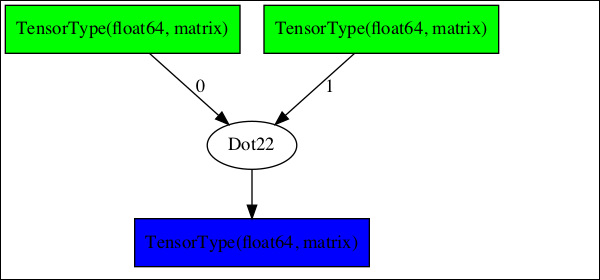
複雜圖形
在較大的表示式中,計算圖可能非常複雜。此處顯示了從 Theano 文件中獲取的一個此類圖形:

要了解 Theano 的工作原理,首先了解這些計算圖的重要性非常重要。有了這種理解,我們將知道 Theano 的重要性。
為什麼要使用 Theano?
透過檢視計算圖的複雜性,您現在將能夠理解開發 Theano 的目的。一個典型的編譯器會在程式中提供本地最佳化,因為它從未將整個計算視為一個單元。
Theano 實施了非常高階的最佳化技術來最佳化完整的計算圖。它將代數的各個方面與最佳化編譯器的各個方面相結合。圖的一部分可以編譯成 C 語言程式碼。對於重複計算,評估速度至關重要,Theano 透過生成非常高效的程式碼來滿足此目的。
Theano - 資料型別
現在,您已經瞭解了 Theano 的基礎知識,讓我們開始瞭解可用於建立表示式的不同資料型別。下表為您提供了 Theano 中定義的資料型別的部分列表。
| 資料型別 | Theano 型別 |
|---|---|
| 位元組 | bscalar、bvector、bmatrix、brow、bcol、btensor3、btensor4、btensor5、btensor6、btensor7 |
| 16 位整數 | wscalar、wvector、wmatrix、wrow、wcol、wtensor3、wtensor4、wtensor5、wtensor6、wtensor7 |
| 32 位整數 | iscalar、ivector、imatrix、irow、icol、itensor3、itensor4、itensor5、itensor6、itensor7 |
| 64 位整數 | lscalar、lvector、lmatrix、lrow、lcol、ltensor3、ltensor4、ltensor5、ltensor6、ltensor7 |
| 浮點數 | fscalar、fvector、fmatrix、frow、fcol、ftensor3、ftensor4、ftensor5、ftensor6、ftensor7 |
| 雙精度浮點數 | 標量,向量,矩陣,行向量,列向量,三階張量,四階張量,五階張量,六階張量,七階張量 |
| 複數 | 複數標量,複數向量,複數矩陣,複數行向量,複數列向量,複數三階張量,複數四階張量,複數五階張量,複數六階張量,複數七階張量 |
以上列表並不完整,請參考張量建立文件以獲取完整列表。
我現在將給出一些關於如何在 Theano 中建立各種資料型別的變數的例子。
標量
要構造一個標量變數,可以使用以下語法:
語法
x = theano.tensor.scalar ('x')
x = 5.0
print (x)
輸出
5.0
一維陣列
要建立一個一維陣列,使用以下宣告:
示例
f = theano.tensor.vector f = (2.0, 5.0, 3.0) print (f)f = theano.tensor.vector f = (2.0, 5.0, 3.0) print (f) print (f[0]) print (f[2])
輸出
(2.0, 5.0, 3.0) 2.0 3.0
如果執行 **f[3]**,則會生成一個索引超出範圍的錯誤,如下所示:
print f([3])
輸出
IndexError Traceback (most recent call last) <ipython-input-13-2a9c2a643c3a> in <module> 4 print (f[0]) 5 print (f[2]) ----> 6 print (f[3]) IndexError: tuple index out of range
二維陣列
要宣告一個二維陣列,可以使用以下程式碼片段:
示例
m = theano.tensor.matrix m = ([2,3], [4,5], [2,4]) print (m[0]) print (m[1][0])
輸出
[2, 3] 4
五維陣列
要宣告一個五維陣列,使用以下語法:
示例
m5 = theano.tensor.tensor5 m5 = ([0,1,2,3,4], [5,6,7,8,9], [10,11,12,13,14]) print (m5[1]) print (m5[2][3])
輸出
[5, 6, 7, 8, 9] 13
可以使用資料型別 **tensor3** 代替 **tensor5** 宣告三維陣列,使用資料型別 **tensor4** 宣告四維陣列,依此類推,直到 **tensor7**。
多元構造器
有時,您可能希望在一個宣告中建立相同型別的多個變數。可以使用以下語法來實現:
語法
from theano.tensor import * x, y, z = dmatrices('x', 'y', 'z')
x = ([1,2],[3,4],[5,6])
y = ([7,8],[9,10],[11,12])
z = ([13,14],[15,16],[17,18])
print (x[2])
print (y[1])
print (z[0])
輸出
[5, 6] [9, 10] [13, 14]
Theano - 變數
在上一章討論資料型別時,我們建立並使用了 Theano 變數。重申一下,可以使用以下語法在 Theano 中建立變數:
x = theano.tensor.fvector('x')
在此語句中,我們建立了一個名為 **x** 的變數,它是一個包含 32 位浮點數的向量。我們也將其命名為 **x**。名稱通常用於除錯。
要宣告一個 32 位整數的向量,可以使用以下語法:
i32 = theano.tensor.ivector
這裡,我們沒有為變數指定名稱。
要宣告一個包含 64 位浮點數的三維向量,可以使用以下宣告:
f64 = theano.tensor.dtensor3
下面表格列出了各種構造器及其資料型別:
| 構造器 | 資料型別 | 維度 |
|---|---|---|
| fvector | float32 | 1 |
| ivector | int32 | 1 |
| fscalar | float32 | 0 |
| fmatrix | float32 | 2 |
| ftensor3 | float32 | 3 |
| dtensor3 | float64 | 3 |
可以使用通用向量構造器並顯式指定資料型別,如下所示:
x = theano.tensor.vector ('x', dtype=int32)
在下一章中,我們將學習如何建立共享變數。
Theano - 共享變數
很多時候,您需要建立在不同函式之間以及同一函式的多次呼叫之間共享的變數。例如,在訓練神經網路時,您會建立一個權重向量,用於為所考慮的每個特徵分配權重。在網路訓練期間的每次迭代中都會修改此向量。因此,它必須在對同一函式的多次呼叫中全域性可用。因此,我們為此目的建立了一個共享變數。通常,Theano 會將此類共享變數移動到 GPU(如果可用)。這可以加快計算速度。
語法
建立共享變數時,可以使用以下語法:
import numpy W = theano.shared(numpy.asarray([0.1, 0.25, 0.15, 0.3]), 'W')
示例
這裡建立了一個包含四個浮點數的 NumPy 陣列。要設定/獲取 **W** 的值,可以使用以下程式碼片段:
import numpy
W = theano.shared(numpy.asarray([0.1, 0.25, 0.15, 0.3]), 'W')
print ("Original: ", W.get_value())
print ("Setting new values (0.5, 0.2, 0.4, 0.2)")
W.set_value([0.5, 0.2, 0.4, 0.2])
print ("After modifications:", W.get_value())
輸出
Original: [0.1 0.25 0.15 0.3 ] Setting new values (0.5, 0.2, 0.4, 0.2) After modifications: [0.5 0.2 0.4 0.2]
Theano - 函式
Theano **function** 充當與符號圖互動的鉤子。符號圖被編譯成高效的執行程式碼。它透過重構數學方程來提高速度。它將表示式的一些部分編譯成 C 語言程式碼。它將一些張量移動到 GPU,等等。
現在將高效的編譯程式碼作為輸入提供給 Theano **function**。當執行 Theano **function** 時,它會將計算結果分配給我們指定的變數。最佳化型別可以指定為 FAST_COMPILE 或 FAST_RUN。這在環境變數 THEANO_FLAGS 中指定。
Theano **function** 使用以下語法宣告:
f = theano.function ([x], y)
第一個引數 **[x]** 是輸入變數列表,第二個引數 **y** 是輸出變數列表。
現在已經瞭解了 Theano 的基礎知識,讓我們用一個簡單的例子開始 Theano 編碼。
Theano - 簡單訓練示例
Theano 在訓練神經網路方面非常有用,在神經網路中,我們必須重複計算成本和梯度以達到最優。在大型資料集上,這會變得計算密集。由於 Theano 對我們之前看到的計算圖進行了內部最佳化,因此可以高效地完成此操作。
問題陳述
現在我們將學習如何使用 Theano 庫來訓練網路。我們將採用一個簡單的案例,從一個包含四個特徵的資料集開始。在對每個特徵應用一定的權重(重要性)後,我們計算這些特徵的總和。
訓練的目標是修改分配給每個特徵的權重,以便總和達到目標值 100。
sum = f1 * w1 + f2 * w2 + f3 * w3 + f4 * w4
其中 **f1**、**f2** 等是特徵值,**w1**、**w2** 等是權重。
為了更好地理解問題陳述,讓我量化一下這個例子。我們將假設每個特徵的初始值為 1.0,並將 w1 等於 **0.1**、**w2** 等於 **0.25**、**w3** 等於 **0.15** 以及 **w4** 等於 **0.3**。分配權重值沒有明確的邏輯,這只是我們的直覺。因此,初始總和如下:
sum = 1.0 * 0.1 + 1.0 * 0.25 + 1.0 * 0.15 + 1.0 * 0.3
總和為 **0.8**。現在,我們將不斷修改權重分配,使此總和接近 100。當前 **0.8** 的結果值距離我們期望的 100 的目標值相差甚遠。在機器學習術語中,我們將 **成本** 定義為目標值減去當前輸出值之差,通常將其平方以放大誤差。我們透過計算梯度並更新權重向量來減少每次迭代中的此成本。
讓我們看看如何在 Theano 中實現整個邏輯。
宣告變數
我們首先宣告我們的輸入向量 x,如下所示:
x = tensor.fvector('x')
其中 **x** 是一個包含浮點值的單維陣列。
我們定義一個標量 **target** 變數,如下所示:
target = tensor.fscalar('target')
接下來,我們建立一個權重張量 **W**,其初始值如上所述:
W = theano.shared(numpy.asarray([0.1, 0.25, 0.15, 0.3]), 'W')
定義 Theano 表示式
我們現在使用以下表達式計算輸出:
y = (x * W).sum()
請注意,在上述語句中,**x** 和 **W** 是向量,而不是簡單的標量變數。我們現在使用以下表達式計算誤差(成本):
cost = tensor.sqr(target - y)
成本是目標值和當前輸出值之差的平方。
要計算梯度(它告訴我們距離目標有多遠),我們使用內建的 **grad** 方法,如下所示:
gradients = tensor.grad(cost, [W])
我們現在透過採用 **0.1** 的學習率來更新 **weights** 向量,如下所示:
W_updated = W - (0.1 * gradients[0])
接下來,我們需要使用上述值更新我們的權重向量。我們在以下語句中執行此操作:
updates = [(W, W_updated)]
定義/呼叫 Theano 函式
最後,我們在 Theano 中定義一個 **function** 來計算總和。
f = function([x, target], y, updates=updates)
要呼叫上述函式一定次數,我們建立一個 **for** 迴圈,如下所示:
for i in range(10): output = f([1.0, 1.0, 1.0, 1.0], 100.0)
如前所述,函式的輸入是一個包含四個特徵的初始值的向量 - 我們將每個特徵的值分配為 **1.0**,沒有任何具體原因。您可以分配您選擇的不同值並檢查函式最終是否收斂。我們將在每次迭代中列印權重向量和相應輸出的值。它在下面的程式碼中顯示:
print ("iteration: ", i)
print ("Modified Weights: ", W.get_value())
print ("Output: ", output)
完整程式清單
為了方便您快速參考,這裡提供了完整的程式清單:
from theano import *
import numpy
x = tensor.fvector('x')
target = tensor.fscalar('target')
W = theano.shared(numpy.asarray([0.1, 0.25, 0.15, 0.3]), 'W')
print ("Weights: ", W.get_value())
y = (x * W).sum()
cost = tensor.sqr(target - y)
gradients = tensor.grad(cost, [W])
W_updated = W - (0.1 * gradients[0])
updates = [(W, W_updated)]
f = function([x, target], y, updates=updates)
for i in range(10):
output = f([1.0, 1.0, 1.0, 1.0], 100.0)
print ("iteration: ", i)
print ("Modified Weights: ", W.get_value())
print ("Output: ", output)
執行程式時,您將看到以下輸出:
Weights: [0.1 0.25 0.15 0.3 ] iteration: 0 Modified Weights: [19.94 20.09 19.99 20.14] Output: 0.8 iteration: 1 Modified Weights: [23.908 24.058 23.958 24.108] Output: 80.16000000000001 iteration: 2 Modified Weights: [24.7016 24.8516 24.7516 24.9016] Output: 96.03200000000001 iteration: 3 Modified Weights: [24.86032 25.01032 24.91032 25.06032] Output: 99.2064 iteration: 4 Modified Weights: [24.892064 25.042064 24.942064 25.092064] Output: 99.84128 iteration: 5 Modified Weights: [24.8984128 25.0484128 24.9484128 25.0984128] Output: 99.968256 iteration: 6 Modified Weights: [24.89968256 25.04968256 24.94968256 25.09968256] Output: 99.9936512 iteration: 7 Modified Weights: [24.89993651 25.04993651 24.94993651 25.09993651] Output: 99.99873024 iteration: 8 Modified Weights: [24.8999873 25.0499873 24.9499873 25.0999873] Output: 99.99974604799999 iteration: 9 Modified Weights: [24.89999746 25.04999746 24.94999746 25.09999746] Output: 99.99994920960002
觀察到經過四次迭代後,輸出為 **99.96**,經過五次迭代後,輸出為 **99.99**,這接近我們期望的 **100.0** 的目標。
根據所需的精度,您可以安全地得出結論,網路在 4 到 5 次迭代中得到訓練。訓練完成後,查詢權重向量,經過 5 次迭代後,權重向量將採用以下值:
iteration: 5 Modified Weights: [24.8984128 25.0484128 24.9484128 25.0984128]
您現在可以在網路中使用這些值來部署模型。
Theano - 結論
機器學習模型構建涉及大量重複計算,這些計算涉及張量。這些需要大量的計算資源。由於常規編譯器會在本地級別提供最佳化,因此通常不會生成快速的執行程式碼。
Theano 首先為整個計算構建一個計算圖。由於整個計算圖在編譯期間作為一個整體可用,因此可以在預編譯期間應用多種最佳化技術,而這正是 Theano 所做的。它重構計算圖,部分將其轉換為 C,將共享變數移動到 GPU,等等,以生成非常快速的執行程式碼。然後,編譯後的程式碼由 Theano **function** 執行,該函式僅充當將編譯後的程式碼注入執行時的鉤子。Theano 已證明其能力,並在學術界和工業界得到廣泛認可。