Sec 60

---

引言

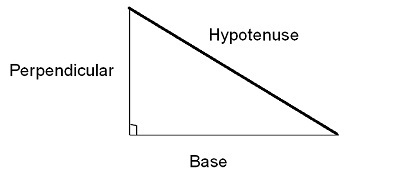
三角學是數學的一個分支，研究直角三角形的邊與角之間的關係。用於研究這種關係的比率稱為三角比率。即正弦、餘弦、正切、餘切、正割、餘割。直角三角形的三個邊分別是斜邊、底邊（鄰邊）和高（對邊），幾何中的三角比由此得出。

“三角學”這個名稱是由“Trigonon”和“Metron”這兩個片語成的，分別表示三角形和測量。在直角三角形中，斜邊長度與鄰邊（底邊）長度的比值稱為一個角的正割。在本教程中，我們將討論 sec60 度的值和三角學。

三角函式

三角函式的主要分支是正切、正弦和餘弦角。此外，可以使用主要函式生成另外三個函式：餘切、正割和餘割。與主要三角函式相比，另外三個函式通常使用得更頻繁。有關這三個主要函式的說明，請參見附圖。三角學通常定義為直角三角形。

正弦函式

斜邊長度與對邊長度（高）之比稱為角度正弦函式。上面三角形的正弦值如下：

$$\mathrm{\sin\theta\:=\:\frac{高}{斜邊}}$$

餘弦函式

它是斜邊長度與鄰邊長度（底邊）之比。從上面提到的三角形中，餘弦函式推導如下：

$$\mathrm{\cos\theta\:=\:\frac{底邊}{斜邊}}$$

正切函式

鄰邊和對邊的長度之比稱為正切函式。

$$\mathrm{\tan\theta\:=\:\frac{高}{底邊}}$$

另外三個函式是從正弦、餘弦和正切基本函式推匯出來的，分別是正割、餘割和餘切。

$$\mathrm{\cot\theta\:=\:\frac{1}{\tan\theta}\:=\:\frac{底邊}{高}}$$

$$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜邊}{底邊}}$$

$$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜邊}{底邊}}$$

三角方程或恆等式是適用於直角三角形的方程。以下是一些特殊的三角公式：

勾股恆等式

$$\mathrm{\sin^{2}\:\theta\:+\:\cos^{2}\:\theta\:=\:1}$$

$$\mathrm{\tan^{2}\:\theta\:+\:1\:=\:\sec^{2}\:\theta}$$

$$\mathrm{\cot^{2}\:\theta\:+\:1\:=\:cosec^{2}\:\theta}$$

$$\mathrm{\sin\:2\theta\:=\:2\sin\:\theta\:\cos\:\theta}$$

$$\mathrm{\cos\:2\theta\:=\:\cos^{2}\theta\:-\:\sin^{2}\:\theta}$$

$$\mathrm{\cos\:2\theta\:=\:\frac{2\:\tan\:\theta}{1\:-\:\tan^{2}\:\theta}}$$

$$\mathrm{\cos\:2\theta\:=\:\frac{\cot^{2}\:\theta\:-\:1}{2\:\cot\:\theta}}$$

和差恆等式

角度 u 和 v 有如下關係：

$$\mathrm{\sin(u\:+\:v)\:=\:\sin(u)\:\cos(v)\:+\:cos(u)\sin(v)}$$

$$\mathrm{\cos(u\:+\:v)\:=\:\cos(u)\:\cos(v)\:-\:sin(u)\sin(v)}$$

$$\mathrm{\sin(u\:-\:v)\:=\:\sin(u)\:\cos(v)\:-\:cos(u)\sin(v)}$$

$$\mathrm{\cos(u\:-\:v)\:=\:\cos(u)\:\cos(v)\:+\:sin(u)\sin(v)}$$

$$\mathrm{\tan(u\:+\:v)\:=\:\frac{\tan(u)\:+\:\tan(v)}{1\:-\:\tan(u)\:\tan(v)}}$$

$$\mathrm{\tan(u\:-\:v)\:=\:\frac{\tan(u)\:-\:\tan(v)}{1\:+\:\tan(u)\:\tan(v)}}$$

正割函式及其影像

在三角學中，正割函式是週期函式。在直角三角形中，斜邊長度與底邊長度之比稱為正割函式或 sec 函式。它也寫成 $\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜邊}{底邊}}$，因為它是的倒數。

因為它是餘弦函式的倒數。由於我們已經熟悉餘弦曲線，所以繪製正割曲線變得非常簡單。透過確定每個餘弦值的倒數，我們可以快速建立 sec x 的圖形。當 cos x 的值很小時，sec x 的值將非常大。具體來說，確定 $\mathrm{\frac{1}{y}}$ 對於直線 $\mathrm{y\:=\:cosx}$ 上的每個 y 值。下表顯示了一些以弧度表示的角度

x	$\mathrm{\cos\:x}$	$\mathrm{\sec\:x}$
0	1	1
$\mathrm{\frac{\pi}{6}}$	$\mathrm{\frac{\sqrt{3}}{2}}$	$\mathrm{\frac{2}{\sqrt{3}}}$
$\mathrm{\frac{\pi}{4}}$	$\mathrm{\frac{1}{\sqrt{2}}}$	$\mathrm{\sqrt{2}}$
$\mathrm{\frac{\pi}{3}}$	$\mathrm{\frac{1}{2}}$	2
$\mathrm{\frac{\pi}{2}}$	0	未定義

此外，我們注意到，當餘弦函式的值為零時，正割函式趨於無窮大，這意味著正割函式在該點未定義。因此，我們得到 sec x 圖如下：

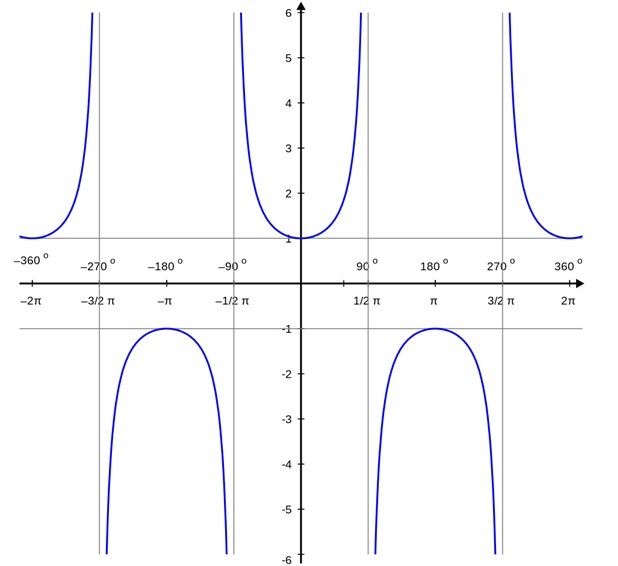
Sec 60

所以，sec 60 度的值為 2。sec 60 度用弧度表示。sec 60 度的 60° 角位於 0° 和 90°（第一象限）之間。sec 60° 值 = 2，因為正割函式在第一象限為正。

鑑於正割函式是一個週期函式，sec 60° 可以表示為

注意 - 正割是一個偶函式，$\mathrm{\sec(-60°)\:等於\:\sec(60°)}$

正割函式的重要性

正割函式是三角學中重要的三角函式之一。一條直線或射線與曲線（特別是圓）相切一次以上，則它等同於直角三角形的斜邊與底邊的比值。正割函式的另一個名稱是餘弦函式的倒數

例題

例1 - 當 $\mathrm{\sec\:\theta}$ 的值為 2 時，求 𝑡𝑎𝑛 𝜃 的值。

解 - 我們知道 $\mathrm{\tan\:\theta}$ 和 $\mathrm{\sec\:\theta}$ 之間的關係是

$$\mathrm{\sec^{2}\:\theta\:=\:1\:+\:tan^{2}\:\theta}$$

$$\mathrm{\tan^{2}\:\theta\:=\:\sec^{2}\:\theta\:-\:1}$$

已知 $\mathrm{\sec\:\theta}$ 的值為 2，現在將此值代入上述方程：

$$\mathrm{\tan^{2}\:\theta\:=\:2^{2}\:-\:1}$$

$$\mathrm{\tan^{2}\:\theta\:=\:4\:-\:1}$$

$$\mathrm{\tan^{2}\:\theta\:=\:3}$$

$$\mathrm{\tan\:\theta\:=\:\sqrt{3}}$$

例2 - 當 𝑠𝑒𝑐𝜃 的值為 1 時，求 𝑡𝑎𝑛𝜃 的值。

解 - 已知 $\mathrm{\sec\:\theta\:=\:1}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\theta\:=\:0°}$

所以，$\mathrm{\tan\:\theta\:=\:\tan0°\:=\:0}$

例3 - 當 𝑠𝑒𝑐𝜃 的值為 1 時，求 𝑐𝑜𝑠 𝜃 的值。

解 - 我們知道 $\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜邊}{底邊}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\cos\:\theta\:=\:\frac{1}{\sec\:\theta}}$

$\mathrm{\:\:正割函式的重要性\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\cos\:\theta\:=\:\frac{1}{1}\:=\:1}$

例4 - 正割函式的定義域是什麼？

解 - 正割函式的定義域是 $\mathrm{R\:-\:(2n\:+\:1)\:\frac{\pi}{2}}$，其中 R 為實數。

例5 - 求 $\mathrm{\cos\:2\theta\:和\:\sec\:\theta}$ 之間的關係

解 - 我們知道 $\mathrm{\cos\:2\theta\:=\:cos^{2}\:\theta\:-\:\sin^{2}\:\theta}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sin^{2}\:\theta\:+\:\cos^{2}\:\theta\:=\:1}$

$\mathrm{\Rightarrow\:\sin^{2}\:\theta\:=\:1\:-\:\cos^{2}\:\theta}$

現在將此值代入上述方程

$\mathrm{\cos\:2\theta\:=\:cos^{2}\:\theta\:-\:(1\:-\:\cos^{2}\:\theta)}$

$\mathrm{\cos\:2\theta\:=\:2\cos^{2}\:\theta\:-\:1}$

我們知道 $\mathrm{\sec\:\theta\:=\frac{1}{\cos\:\theta}}$ 將此值代入上述方程

$\mathrm{\cos\:2\theta\:=\:\frac{2}{\sec^{2}\:\theta}\:-\:1}$

例6 - 求 $\mathrm{2\tan\:45°\:+\:\sec\:60°}$ 的值

解 - $\mathrm{2\tan\:45°\:+\:\sec\:60°}$

現在代入它們的值 $\mathrm{2\tan\:45°\:+\:\sec\:60°\:=\:2\:+\:2}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:4}$

例7 - 化簡 $\mathrm{\frac{\sec^{2}\:60°\:+\:\tan\:45°}{2\tan\:45°}}$

解 - 給定的方程是 $\mathrm{\frac{\sec^{2}\:60°\:+\:\tan\:45°}{2\tan\:45°}}$

我們知道 $\mathrm{\tan\:45°}$ 的值為 1，𝑠𝑒𝑐60° 的值為 2

所以，$\mathrm{\frac{\sec^{2}\:60°\:+\:\tan\:45°}{2\tan\:45°}\:=\:\frac{4\:+\:1}{2}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{5}{2}}$

例8 - 化簡 $\mathrm{\sec60°\:-\:\cos60°}$

解 - 給定的方程是 $\mathrm{\sec60°\:-\:\cos60°}$

$\mathrm{\Rightarrow\:2\:-\:\frac{1}{2}}$

$\mathrm{\Rightarrow\:\frac{3}{2}}$

例9 - 化簡 $\mathrm{\frac{\sec60°}{\cos60°}\:-\:\frac{\cos60°}{\sec60°}}$

解 - 給定的方程是 $\mathrm{\frac{\sec60°}{\cos60°}\:-\:\frac{\cos60°}{\sec60°}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\frac{2}{\frac{1}{2}}\:-\:\frac{\frac{1}{2}}{2}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:4\:-\:\frac{1}{4}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\frac{15}{4}}$

結論

60度角的正割三角函式值是2。在直角三角形中，斜邊長度與底邊長度之比稱為正割函式或 sec 函式。它也寫成 $\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜邊}{底邊}}$，因為它是的倒數

常見問題

1. 正割函式是什麼意思？

在直角三角形中，斜邊長度與底邊長度之比稱為正割函式或 sec 函式

2. 三角學是什麼意思？

三角形的邊長比與角度之間的關係是三角學這個數學分支的研究物件。

3. 60度時正割函式的值是多少？

60度角的正割三角函式值（Sec 60度）為2。

4. 求正割函式的奇偶性？

正割函式是偶函式，因為對於所有x，$\mathrm{\sec(-x)\:=\:\sec\:x}$。

5. 餘弦函式和正割函式之間有什麼關係？

正割函式也可以寫成$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜邊}{底邊}}$，因為它是餘弦函式的倒數。