資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究三相感應電動機中的旋轉磁場
當三相電源饋送到三相感應電動機的定子繞組時，會產生旋轉磁場 (RMF)。該磁場使得其磁極不會停留在定子上固定的位置，而是不斷地圍繞定子改變其位置。因此，它被稱為旋轉磁場 (RMF) 或 RMF。
在數學上，可以證明該旋轉磁場的幅值是恆定的，並且等於任何相位電流產生的最大磁通量 (ϕm) 的 1.5 倍。
旋轉磁場的速度稱為同步速度 (NS)。同步速度的值取決於定子上的磁極數 (P) 和電源頻率 (f)。因此，
$$\mathrm{同步速度, 𝑁_𝑆 =\frac{120 𝑓}{𝑃}RPM}$$
旋轉磁場的數學分析
考慮三個相同的線圈，它們在空間上彼此相隔 120°。假設這三個線圈由平衡的三相電源供電。因此，每個線圈都會在其自身軸線上產生交變磁通量。現在，假設三個瞬時磁通量分別為：
$$\mathrm{\varphi_1 = \varphi_m sin \omega t … (1)}$$
$$\mathrm{\varphi_2 = \varphi_m sin(\omega t − 120°) … (2)}$$
$$\mathrm{\varphi_3 = \varphi_m sin(\omega t + 120°) … (3)}$$
這裡，ϕm 是任何相位電流產生的磁通量的最大值。相量圖顯示了這三個磁通量。
為了確定合成磁通量的幅值，將每個磁通量分解成水平和垂直分量，然後求其相量和。
因此，磁通量的合成水平分量由下式給出：
$$\mathrm{\varphi_h = \varphi_1 − \varphi_2 cos 60° − \varphi_3 cos 60° = \varphi_1 − (\varphi_2 + \varphi_3) cos 60°}$$
$$\mathrm{⇒ \varphi_h = \varphi_1 −\frac{1}{2}(\varphi_2 + \varphi_3)}$$
$$\mathrm{⇒ \varphi_h = (\varphi_m sin \omega t) −\frac{1}{2}[\varphi_m sin(\omega t − 120°) + \varphi_m sin(\omega t + 120°)]}$$
$$\mathrm{⇒ \varphi_h = (\varphi_m sin \omega t) −\frac{\varphi_m}{2}(sin \omega t\:cos 120° − cos \omega t\:sin 120°+ sin \omega t\:𝑐𝑜𝑠120° + cos \omega t\:sin 120°)}$$
$$\mathrm{⇒ \varphi_h = \varphi_m sin \omega t − [\frac{\varphi_m}{2}× (2 sin \omega t) × (\frac{-1}{2})]}$$
$$\mathrm{⇒ \varphi_h =\frac{3}{2}\varphi_m sin \omega t … (4)}$$
磁通量的合成垂直分量由下式給出：
$$\mathrm{\varphi_v = 0 − \varphi_2 cos 30° + \varphi_3 cos 30° = (−\varphi_2 + \varphi_3) cos 30°}$$
$$\mathrm{⇒ \varphi_v = [−\varphi_m sin(\omega t − 120°) + \varphi_m sin(\omega t + 120°)] cos 30°}$$
$$\mathrm{⇒ \varphi_v =\frac{\sqrt{3}}{2}\varphi_m [−(sin \omega t\:cos 120° − cos \omega t\:sin 120°)+(sin \omega t \:𝑐𝑜𝑠120° + cos \omega t\:sin 120°)]}$$
$$\mathrm{⇒ \varphi_v =\frac{\sqrt{3}}{2}\varphi_m(2 cos \omega t\:sin 120°) =\frac{\sqrt{3}}{2}\varphi_m × (2 cos \omega t) ×\frac{\sqrt{3}}{2}}$$
$$\mathrm{⇒ \varphi_v =\frac{3}{2}\varphi_m cos \omega t … (5)}$$
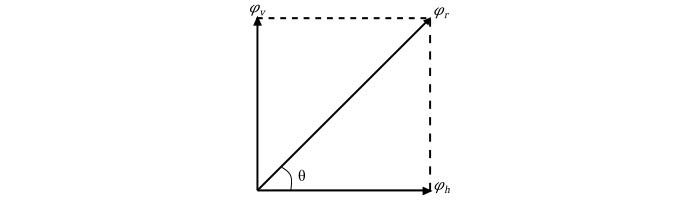
因此，合成磁通量由下式給出：
$$\mathrm{\varphi_r = \sqrt{\varphi_h^2 + \varphi_v^2} = \sqrt{(\frac{3}{2}\varphi_m sin \omega t)^2+ (\frac{3}{2}\varphi_m cos \omega t)^2}}$$
$$\mathrm{⇒ \varphi_r =\frac{3}{2}\varphi_m (\sqrt{sin2 \omega t + cos2 \omega t}) =\frac{3}{2}\varphi_m … (6)}$$
因此，從公式 (6) 可以清楚地看出，合成旋轉磁場的幅值等於每相磁通量 (ϕm) 最大值的 1.5 倍。此外，合成磁通量 (ϕr) 與時間無關，即它是恆定磁通量。
再次，
$$\mathrm{tan \theta =\frac{\varphi_v}{\varphi_h}=\frac{(\frac{3}{2}\varphi_m cos \omega t)}{(\frac{3}{2}\varphi_m sin \omega t)}= cot \omega t = tan(90° − \omega t)}$$
$$\mathrm{\therefore \theta = (90° − \omega t) … (7)}$$
公式 (7) 表明該角度是時間的函式。因此，
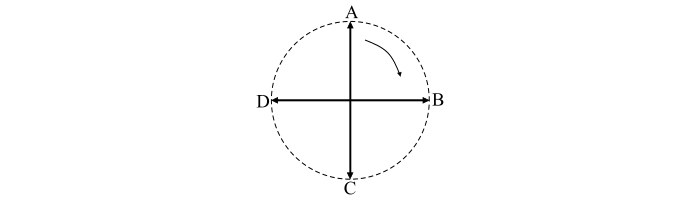
- 情況 1 – 當 ωt = 0° 時；θ = 90°。它對應於上圖中的位置 A。
- 情況 2 – 當 ωt = 90° 時；θ = 0°。它對應於位置 B。
- 情況 3 – 當 ωt = 180° 時；θ = -90°。它對應於位置 C。
- 情況 4 – 當 ωt = 270° 時；θ = -180°。它對應於位置 D。
因此，可以看出合成磁通量在空間中以 ω 弧度/秒的角速度沿順時針方向旋轉。因此，對於具有 P 個磁極的機器，
$$\mathrm{\omega = 2𝜋𝑓;\: and\: 𝑓 =\frac{𝑃𝑁_𝑆}{120};}$$
從以上討論中可以得出以下結論 -
- 平衡三相電源系統的三相電流在電機中產生幅值恆定的合成磁通量。磁通量在每個時刻的幅值為 1.5 ϕm。
- 合成磁通量本質上是旋轉的，並且其旋轉角速度與電源電流的角速度相同。
- 合成磁通量的旋轉方向取決於電源系統的相序。
30K+ 次檢視
