機器學習中的穩健相關性

---

在本教程中，我們將學習機器學習中的穩健相關性。瞭解和評估不同的相關性在各種業務中都很有用。

什麼是相關性？

兩個實體之間的統計關係稱為相關性。或者說，它描述了兩個變數的運動之間的關係。相關性也可以使用不同的資料集。在某些情況下，您可能已經猜到某些事件將如何相互關聯，但在其他情況下，相關性可能會讓您感到意外。重要的是要認識到相關性並不意味著因果關係。散點圖是資料擬合的一個例子。一般來說，可以使用散點圖來評估變數之間是否存在相關性。

不同型別的相關性

正相關

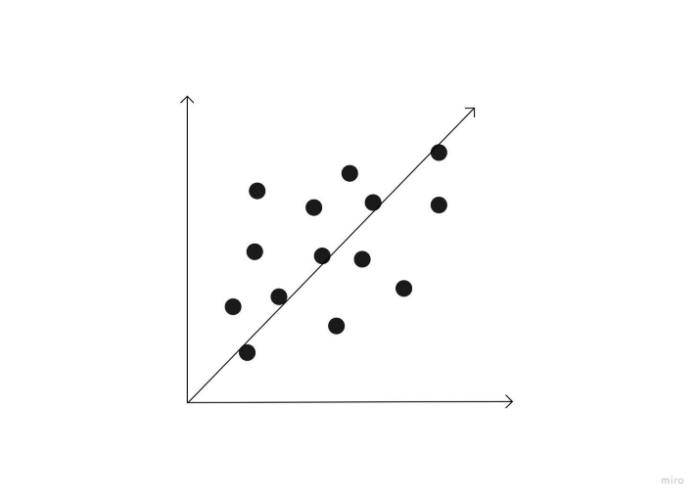
如果關係中的兩個變數都朝相同的方向移動，則該關係被稱為正相關。因此，當一個變數隨著另一個變數的增加而增加，或者當一個變數隨著另一個變數的減少而減少時。身高和體重是兩個顯示正相關關係的變數。

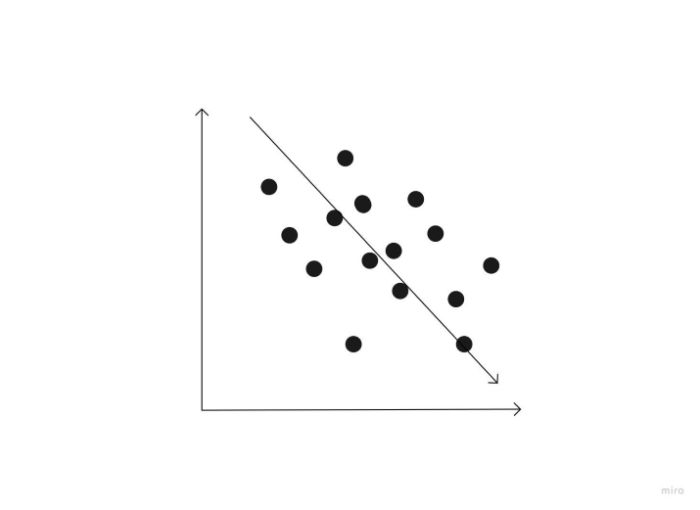
負相關

負相關是兩個變數之間的關係，其中一個變數的增加會導致另一個變數的減少。海拔高度和溫度是負相關的兩個例子。當你爬山（高度增加）時，氣溫會下降（溫度下降）。

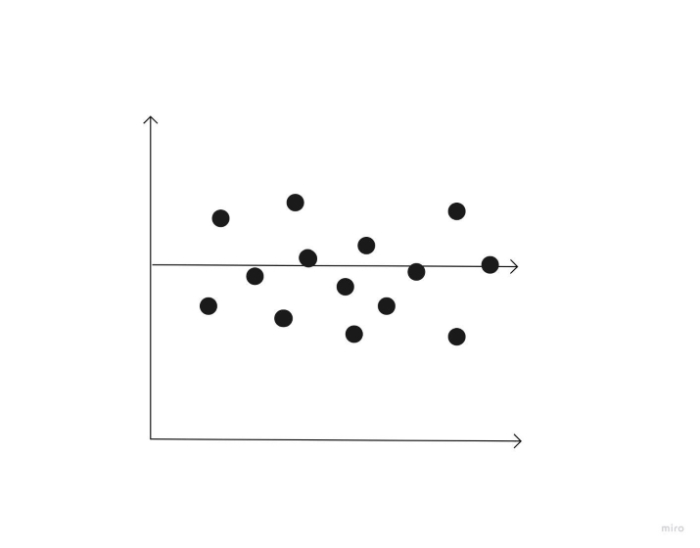
零相關

0 的相關性表示兩個變數之間沒有關係。換句話說，當一個變數朝一個方向移動時，另一個變數朝完全不同的方向移動。

什麼是相關係數？

相關係數是指一個變數的值的變化在多大程度上可以預測另一個變數的值的變化的統計量度。當可以透過另一個變數的變化準確預測一個變數的變化時，人們傾向於假設一個變數的變化一定是另一個變數變化的結果。然而，相關性並不能證明因果關係。這兩個變數都可能受到某個未知因素的類似影響。在消費者資料模式方面，瞭解相關性和因果關係之間的區別可能很有用，並提供有見地的資訊。

相關係數評估兩個變數之間的相關程度，而相關性分析兩個事物如何相互關聯。統計學中存在三種不同的相關係數。

其中一些是：

• 皮爾遜相關性 - 皮爾遜相關性是最常用的確定兩個變數之間是否存線上性關係的方法。根據這兩個資料集的相關性強弱，它將更接近 +1 或 -1。例如，在確定兩隻證券之間如何相互關聯時，皮爾遜 r 相關性用於評估兩隻證券之間股票市場相關性的程度。

• 斯皮爾曼相關性 - 此類相關性用於確定兩個資料集之間的單調關係或聯絡。與皮爾遜相關係數不同，它使用偏斜或有序變數而不是正態分佈變數，並且基於每個資料集的排名值。當變數至少以有序尺度進行評估時，它是合適的相關性分析。此係數需要一個數據表，其中包含原始資料、其排名以及兩個排名之間的差異。

• 肯德爾相關性 - 此類相關性評估兩個資料集之間相互依賴的程度。肯德爾等級相關性是一種非引數檢驗，用於評估兩個變數之間的依賴程度。

您將使用哪種形式的相關係數取決於您對變數的瞭解。使用適當的相關方程將提高您理解正在檢查的資料集之間關係的能力。

公式相關性

要確定相關性，請使用以下公式：

$$\mathrm{\frac{(x(i) − x)(y(i) − \bar{y})}{\sum(x(i) − \bar(x))^2 \: \sum(y(i) − (\bar{y}))^2}}$$

考慮以下表示形式以確定相關性：

• x(i) = x 的值
• y(i) = y 的值
• x̅= x 值的平均值
• ȳ= y 值的平均值

如何計算相關性？

可以使用多種技術來計算相關性。此頁面詳細介紹了最常用的技術，即皮爾遜積矩相關性。皮爾遜積矩相關性分析一對變數的線性關係。任何具有有限協方差矩陣的資料集都適合使用它。

以下是計算相關性的步驟。

• 收集 x 變數和 y 變數的資訊。

• 應確定 x 均值變數以及 y 均值變數。

• 從 x 變數的每個值中減去 x 變數的平均值。對 y 變數重複此過程。

• 將 x 變數的平均值與值之間的每個差異除以 y 變數中相應的差異。

• 透過對這些差異中的每一個求平方來新增答案。

• 計算步驟 5 中值的平方根。

• 將步驟 4 的結果除以步驟 6 的結果。

結論

透過觀察和比較消費者對各種營銷策略的反應，營銷專家利用相關性分析來評估廣告系列的有效性。他們能夠更好地理解並以這種方式幫助他們的客戶。

對於根本原因分析，相關性分析非常有用，並且減少了資料科學家和負責監控資料的人員的發現時間 (TTD) 和修復時間 (TTR)。透過同時或以相同的速度觀察兩個意外事件或異常情況，可以更容易地找到問題的原因。如果能夠儘早識別和解決問題，則組織的成本將降低。

相關性通常用於心理學研究，但是，重要的是要認識到相關性並不意味著因果關係。如果您喜歡處理資料，它是您最好的朋友。它假設一個可能不存在的因果關係，並且是那些不熟悉統計學的人常犯的一個錯誤。