資料結構
網路
關係型資料庫管理系統 (RDBMS)
作業系統
Java
Microsoft Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
JavaScript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學機器學習中的最大似然估計
簡介
最大似然法是一種常用的密度估計方法，它定義了一個似然函式來獲取分佈資料的機率。學習和理解最大似然法的概念至關重要，因為它是學習其他高階機器學習和深度學習技術和演算法的必要核心概念之一。
在本文中，我們將討論似然函式、其背後的核心思想以及它如何結合程式碼示例工作。這將有助於更好地理解這個概念並在需要時應用它。
讓我們先深入瞭解似然函式，以便理解最大似然估計。
什麼是似然？
在機器學習中，似然是衡量資料觀測值的一種指標，它可以告訴我們對於特定資料點，結果或目標變數的值。簡單來說，顧名思義，似然函式告訴我們特定資料點與現有資料分佈的匹配程度。
例如，假設資料集中有兩個資料點。如果第一個資料點的似然值大於第二個資料點，那麼可以假設第一個資料點為最終模型提供了更準確的資訊，因此對於模型來說更有價值和精確。
在討論之後，你可能會產生一個疑問：如果似然函式的工作方式與機率函式相同，那麼它們有什麼區別呢？
機率和似然的區別
雖然機率和似然的工作原理和直覺看起來相同，但存在細微的差別：似然是一個函式，它定義或告訴我們特定資料點在資料分佈中有多大的價值以及對最終演算法的貢獻程度，以及它對機器學習演算法的適用性。
而機率，簡單來說，是一個描述某事件或事物發生的機率的術語，通常是相對於其他情況或條件而言的，大多被稱為條件機率。
此外，與特定問題相關的所有機率之和為1，且不能超過1，而似然值可以大於1。
什麼是最大似然估計？
在討論了似然函式的直覺之後，我們清楚地知道，每個模型都需要更高的似然值才能獲得準確的模型和準確的結果。因此，這裡“最大似然”這個術語表示我們正在最大化似然函式，稱為**似然函式的最大化**。
讓我們嘗試用一個例子來理解。
假設我們有一個分類資料集，其中自變數是學生在特定考試中取得的分數，而目標變數或因變數是分類變數，具有“是”和“否”屬性，表示學生是否在校園招聘中被錄用。
現在，如果我們嘗試使用最大似然估計來解決這個問題，該函式將首先根據目標變數的每個適用條件計算每個資料點的機率。在下一步中，該函式將在二維圖中繪製所有資料點，並嘗試找到最適合資料集的線，將其分成兩部分。最佳擬合線將在一些迭代後獲得，一旦獲得，該線將透過簡單地將其繪製到圖中來對資料點進行分類。
最大似然：基礎
最大似然估計是用於解決分類問題的某些機器學習和深度學習方法的基礎。一個例子是邏輯迴歸，其中該演算法用於使用圖上最佳擬合線對資料點進行分類。關於深度學習演算法，同樣的方法被稱為感知器技巧。
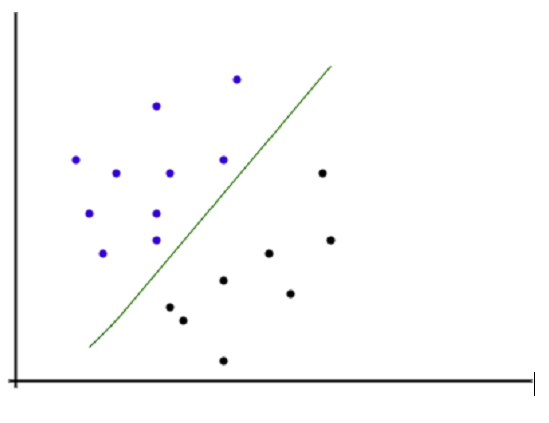
如上圖所示，所有資料觀測值都繪製在二維圖中，其中X軸表示自變數或訓練資料，Y軸表示目標變數。繪製一條線來分離正負資料觀測值。根據演算法，落線上以上的資料點被視為正資料點，落線上以下的資料點被視為負資料點。
最大似然估計：程式碼示例
我們可以使用邏輯迴歸快速實現任何分類資料集的最大似然估計技術。讓我們嘗試實現它。
import pandas as pd import numpy as np import seaborn as sns from sklearn.linear_model import LogisticRegression lr=LogisticRegression() lr.fit(X_train,y_train) lr_pred=lr.predict(X_test) sns.regplot(x="X",y='lr_pred',data=df_pred ,logistic=True, ci=None)
以上程式碼將針對給定的資料集擬合邏輯迴歸，並生成資料的線圖，表示資料的分佈以及根據演算法獲得的最佳擬合。
關鍵要點
最大似然是一個函式，它描述了資料點及其與模型的最佳擬合程度。
最大似然與機率方法不同，機率方法基於計算機率的原理。相反，似然方法試圖根據資料分佈最大化資料觀測值的似然。
最大似然法是一種用於解決密度分佈問題的演算法，是某些演算法（如邏輯迴歸）的基礎。
這種方法非常相似，在深度學習方法中主要被稱為感知器技巧。
結論
在本文中，我們討論了似然函式、最大似然估計、其核心直覺和工作機制，以及一些關鍵要點相關的實際示例。這將幫助人們更好地更深入地理解最大似然，並有效地回答相關面試問題。
14K+ 次瀏覽
