資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟
心理學
社會科學
時裝科學
法律科學Python 程式用於計算第 n 項斐波那契數
在本文中，我們將計算第 n 項斐波那契數。
斐波那契數由以下遞迴關係定義：
Fn = Fn-1 + Fn-2
其中 F0 = 0，F1 = 1。
前幾個斐波那契數為
0,1,1,2,3,5,8,13,..................
我們可以使用遞迴法和動態規劃法來計算斐波那契數。
現在讓我們看看 Python 指令碼形式的實現
方法 1：遞迴法
示例
#recursive approach
def Fibonacci(n):
if n<0:
print("Fibbonacci can't be computed")
# First Fibonacci number
elif n==1:
return 0
# Second Fibonacci number
elif n==2:
return 1
else:
return Fibonacci(n-1)+Fibonacci(n-2)
# main
n=10
print(Fibonacci(n))輸出
34
下面顯示了宣告的所有變數的範圍。
方法 2：動態規劃法
示例
#dynamic approach
Fib_Array = [0,1]
def fibonacci(n):
if n<0:
print("Fibbonacci can't be computed")
elif n<=len(Fib_Array):
return Fib_Array[n-1]
else:
temp = fibonacci(n-1)+fibonacci(n-2)
Fib_Array.append(temp)
return temp
# Driver Program
n=10
print(fibonacci(n))輸出
34
下面顯示了宣告的所有變數的範圍
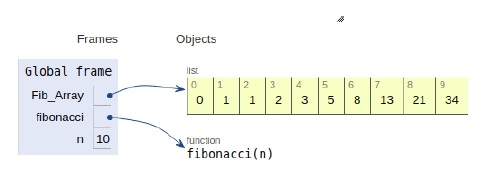
結論
在本文中，我們學習了使用遞迴法和動態規劃法計算第 n 項斐波那契數。
更新日期：11-9-2019
1K+ 檢視次數
廣告