C++程式：求直線的斜率

---

在本文中，我們將學習如何使用程式找到直線的斜率。但在進入程式之前，讓我們首先了解直線的斜率在數學中代表什麼，以及如何在 C++ 中使用其數學公式來計算它。

在數學中，直線的斜率是一個數值，用於衡量直線的傾斜度和方向。它表示當您沿直線從左到右（或水平）移動時，直線上升或下降的速率。通常用字母“m”表示。在數學中，傾斜度指的是直線的斜率或梯度。

從數學角度來說，它代表直線上任意兩點之間垂直方向（y 軸）的變化量與水平方向（x 軸）的變化量的比值。這個比值可以表示為m = y 的變化量 / x 的變化量。

要找到直線的斜率，您必須知道直線上的兩個點。假設這兩個點是 (x1, y1) 和 (x2, y2)。然後，斜率 m 計算如下：

Slope (m) = (Y2 - Y1)/(X2 - X1)

讓我們透過輸入和輸出場景來了解輸入值如何與所需的輸出相關聯：

輸入

p1(-1, 1),  p2(3, 3)

輸出

0.5

說明

使用斜率 (m) 公式 =(Y2 - Y1)/(X2 - X1)，假設值為

x1 = -1, y1 = 1
x2 = 3,  y2 = 3
The slope of line = 1/2 = 0.5

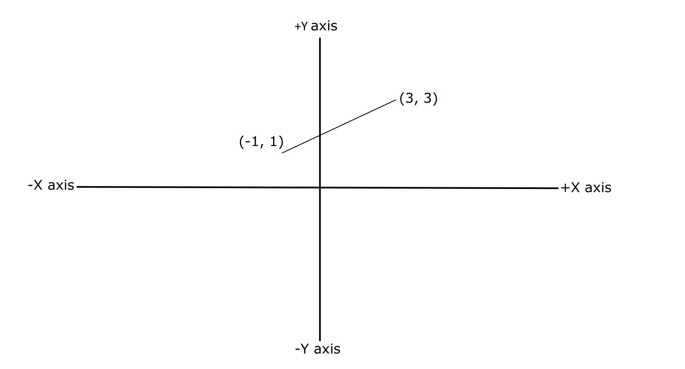
下圖中，我們繪製了一條直線的斜率，並標出了兩個點，分別為 (x1, y1) 和 (x2, y2) 軸值。程式中將使用相同的點值來求直線的斜率：

以下是查詢直線斜率的分步過程：

確定直線上具有值的兩個座標。為了簡化此表示式，我們可以將它們稱為 (x1, y1) 和 (x2, y2)。

透過減去兩個點的 y 座標來計算垂直方向的變化量 (Δy)。

Δ𝑦=y2−y1.

透過減去兩個點的 x 座標來計算水平方向的變化量 (Δ𝑥)。

Δx=x2−x1.

為了找到直線的斜率，我們將使用定義的幾何公式，使用位於直線上的任意兩點 p1(x1, y1) 和 p2(x2, y2) 來求直線的斜率。

Slope (m) = Δy/Δx = y2−y1/ x2−x1 (Here Δ𝑥 and Δ𝑦 means change in movement.)

示例

以下是使用 C++ 查詢直線斜率的程式：

#include <iostream>
#include <iomanip> 
using namespace std;
float calcSlope(float point[2][2]){
   float slope = ((point[1][1] - point[0][1]) / (point[1][0] - point[0][0]));
   return slope;
}
int main() {
   float points[2][2] = {{-1, 1}, {3, 3}};
   cout << "The slope of the line is " << fixed << setprecision(2) << calcSlope(points) << endl;
   return 0;
}

輸出

The slope of the line is 0.50

以下是一些關於直線斜率的關鍵點：

• 根據直線如何傾斜向上、傾斜向下或沒有形狀，斜率可以是正數、負數、零或未定義。
• 如果斜率為正，則直線將從左到右向上傾斜。從左到右移動將是一系列的增加。
• 如果斜率仍然為零，則直線是水平的。但是，此斜率也可能導致未定義的斜率，這意味著直線是垂直的。