資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟
心理學
社會研究
時尚研究
法律研究用 C++ 列印所有從根節點到子節點的路徑以及其相對位置
針對本問題，我們給定了一棵二叉樹。我們需要列印從樹的根節點到子節點的所有路徑。同時，使用下劃線“_”表示節點的相對位置。
讓我們用一個示例來更好地理解這個主題 −
輸入 −
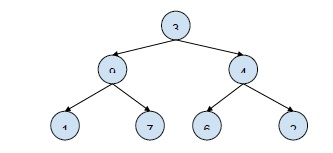
輸出 −
_ _ 3 _ 9 1 _3 9 _7 3 _ 4 _ _ 2 3 9 4 1 7 6 2 3 _ 4 6
為了解決這個問題，我們將利用樹的元素的垂直順序概念。
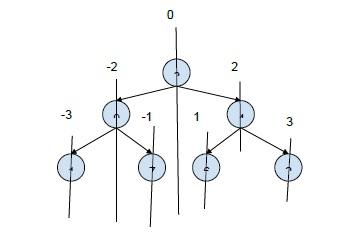
基於這個概念，我們將列印從根節點到子節點的路徑。
演算法
Step 1: Traverse the binary tree using preorder traversal. And on traversal calculate the horizontal distance based on the order. The horizontal distance of root is 0 and processed as the above diagram. Step 2: And on traversing to the leaf node, print the path with an underscore “_” at the end.
示例
#include<bits/stdc++.h>
using namespace std;
#define MAX_PATH_SIZE 1000
struct Node{
char data;
Node *left, *right;
};
Node * newNode(char data){
struct Node *temp = new Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
struct PATH{
int horizontalDistance;
char key;
};
void printPath(vector < PATH > path, int size){
int minimumhorizontalDistance = INT_MAX;
PATH p;
for (int it=0; it<size; it++){
p = path[it];
minimumhorizontalDistance = min(minimumhorizontalDistance, p.horizontalDistance);
}
for (int it=0; it < size; it++){
p = path[it];
int noOfUnderScores = abs(p.horizontalDistance -minimumhorizontalDistance);
for (int i = 0; i < noOfUnderScores; i++) cout<<"_ ";
cout<<p.key<<endl;
}
cout<<"\nNext Path\n";
}
void printAllRtLPaths(Node *root, vector < PATH > &AllPath, int horizontalDistance, int order ){
if(root == NULL)
return;
if (root->left == NULL && root->right == NULL){
AllPath[order] = (PATH { horizontalDistance, root->data });
printPath(AllPath, order+1);
return;
}
AllPath[order] = (PATH { horizontalDistance, root->data });
printAllRtLPaths(root->left, AllPath, horizontalDistance-1, order+1);
printAllRtLPaths(root->right, AllPath, horizontalDistance+1, order+1);
}
void printRootToLeafPath(Node *root){
if (root == NULL)
return;
vector<PATH> Allpaths(MAX_PATH_SIZE);
printAllRtLPaths(root, Allpaths, 0, 0);
}
int main(){
Node *root = newNode('3');
root->left = newNode('9');
root->right = newNode('4');
root->left->left = newNode('1');
root->left->right = newNode('7');
root->right->left = newNode('6');
root->right->right = newNode('2');
printRootToLeafPath(root);
return 0;
}輸出
_ _ 3 _ 9 1 Next Path _ 3 9 _ 7 Next Path 3 _ 4 6 Next Path 3 _ 4 _ _ 2
更新日期： 17-Jan-2020
114 次瀏覽
廣告