數學歸納法的原理

---

簡介

數學歸納法涉及一些原理，這些原理是一種特殊的技巧，用於證明代數中以 n 表示的定理和陳述；其中 n 屬於自然數。在數學歸納法中，任何陳述都首先證明 n=1 的情況，然後證明對於任何變數都成立。

什麼是 PMI？

數學歸納法可以描述為一種工具，用於證明任何陳述 A(n)，該陳述對於自然數 n=1、2、3、4、5......n 都成立。數學歸納法基於一些稱為數學歸納法原理 (PMI) 的原理。

為了證明關於陳述 A(n) 的結果，我們可以使用數學歸納法的原理。首先，我們檢查該陳述是否對 A(1) 成立。然後，如果該陳述對 A(1) 成立，我們假設它也對 A(x) 成立，其中 x 表示直到 x 的所有數字，並將相同的假設應用於 A(x+1) 也成立。如果 A(x+1) 成立，則陳述 A(x) 對所有自然數都成立。

數學歸納法的第一個原理

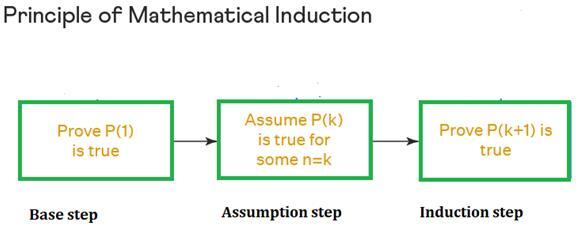
讓我們深入瞭解數學歸納法的第一個原理，並學習用於證明該陳述的步驟。

假設有一個陳述 A(n)，其中 n 屬於自然數。

現在讓我們證明如果該陳述對 n = 1 成立，即如果 A(1) 成立與否。

如果該陳述對 n=1 成立，那麼我們檢查該陳述對 n = x 是否成立，其中 x 是一個自然數。

如果該陳述對 n =x 成立，那麼該等式對 $\mathrm{P(x\:+\:1)}$ 也成立。因此，可以確定陳述 A(n) 對 $\mathrm{n\:\varepsilon\:N}$ 成立。

例題解析

現在讓我們看一個基於第一個 PMI 的例子。

讓我們假設一個陳述 $\mathrm{n\:\varepsilon\:N}$

$$\mathrm{1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:=\:n^{2}}$$

答案 −

令給定陳述 A(n) 定義為 $\mathrm{A(n)\:\colon\:1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:=\:n^{2}}$ ，其中 $\mathrm{n\:\varepsilon\:N}$

基礎步驟 - 注意 A(1) 成立

因為透過將 n=1 代入，我們得到

$\mathrm{1\:=\:1^{2}}$

假設步驟 - 假設 A(x) 對某個 $\mathrm{x\:\varepsilon\:N}$ 成立，

即，$\mathrm{A(x)\:\colon\:1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:=\:x^{2}}$

歸納步驟 - 為了證明 P(x + 1) 成立，

$\mathrm{A(x)\:\colon\:1\:+\:3\:+\:5\:+\:......\:+\:(2n\:-\:1)\:+\:(2n\:+\:1)\:=\:x^{2}\:+\:(2x\:+\:1)}$

$$\mathrm{=\:x^{2}\:+\:2x\:+\:1\:=\:(x\:+\:1)^{2}}$$

因此，當 $\mathrm{x\:\varepsilon\:N}$ 時，A(x + 1) 成立。因此，A(x) 對某個 $\mathrm{x\:\varepsilon\:N}$ 成立

因此，根據 PMI，A(n) 對所有自然數都成立。

數學歸納法的第二個原理

現在我們已經瞭解了第一個 PMI，讓我們瞭解一下第二個 PMI 是什麼以及它可以在哪裡使用。假設我們有一個數學表示式 A(n)，它對所有 n ∈ N 都成立。我們知道證明的步驟是，如果該表示式對 A(1) 成立，然後對任何數字 x 成立，那麼它必須對 P(x+1) 成立。當我們嘗試在考慮複合數後證明它時，問題就出現了。例如，如果我們假設 A(29) 是一個成立的表示式，並且我們必須使用它來證明 P(30) 也成立。如果我們將 30 因式分解為 30 = 2 × 15，則 A(29) 成立的表示式不能用於證明 A(30) 也成立。

因此，我們需要第二個原理來證明歸納法。我們假設一個表示式成立，並用它來證明它對下一個數字也成立。第二個原理背後的邏輯是我們假設該表示式對所有先前的表示式都成立，並用它來證明下一個表示式也成立。在第二個原理中，我們根據自然數的子集陳述該陳述。在許多情況下，我們將使用 I=1 或 I=0。

令 I 為任何整數，S 是 Y 的一個子集，使得

• $\mathrm{I\:\varepsilon\:N}$

• 對於每個 $\mathrm{x\:\varepsilon\:Y}$，其中 $\mathrm{x\:\varepsilon\:Y}$，如果 $\mathrm{\lbrace\:n\:\varepsilon\:Y\:|\:n\:\geq\:I\:\rbrace\:\subseteq\:S}$

例題解析

1) 對於一個數學陳述 $\mathrm{n\:=\:3a\:+\:5b}$，找出存在哪些自然數 (n) 使得整數 a 和 b 為非負整數？

答案 −

令陳述 A(n) 對 $\mathrm{n\:=\:3a\:+\:5b}$ 成立，其中 $\mathrm{a\:\geq\:0\:or\:b\:\geq\:0}$

讓我們看看該陳述是否對 a=0 和 b=0 成立。

$$\mathrm{n\:=\:3\:\times\:0\:+\:5\:\times\:0\:=\:0}$$

所以它不成立。

現在例如，如果 $\mathrm{a\:>\:0}$，即 $\mathrm{a\:=\:1\:,\:b\:=\:0}$

那麼 $\mathrm{3\times\:1\:+\:5\times\:0\:=\:3}$

如果 $\mathrm{b\:>\:0}$，即，$\mathrm{b\:=\:1\:,\:a\:=\:0}$

那麼 $\mathrm{3\times\:0\:+\:5\times\:1\:=\:5}$

因此，我們可以說，如果 a>0 或 b>0，則 $\mathrm{3a\:+\:5b\:\geq\:3}$

但我們看到 A(7) 不成立。

如果我們必須證明 A(8) 是否成立，我們不能使用 A(7) 來證明它。

A(8) 對 a=1 和 b=1 成立，因為 $\mathrm{3\times\:1\:+\:5\times\:1\:=\:8}$

因此，我們可以說，對於每個 $\mathrm{n\:\varepsilon\:N\:with\:n\:\geq\:8}$，都存在非負整數 a 和 b，使得

$$\mathrm{n\:=\:3a\:+\:5b.}$$

結論

數學歸納法是證明一個數學陳述對於所有自然數 n 是否成立的概念。數學歸納法以原理的形式進行推廣。數學歸納法涉及一些原理，這些原理是一種特殊的技巧，用於證明代數中以 n 表示的定理和陳述；其中 n 屬於自然數。在數學歸納法中，任何陳述都首先證明 n=1 的情況，然後證明對於任何變數都成立。為了證明一個陳述，有兩個原理

基礎步驟 - 在此步驟中，我們證明 A(1) 是否成立。

假設步驟 - 在第二步中，我們假設 A(x) 對自然數 x 成立。歸納步驟：在最後一步中，我們證明 $$\mathrm{A(x\:+\:1)} 是否成立。

如果所有步驟都成立，那麼我們可以說“使用 PMI，P(n) 對所有自然數都成立”。

常見問題

1. 第一個 PMI 中的步驟名稱是什麼？

第一個 PMI 中涉及的步驟是基礎步驟、假設步驟和歸納步驟

2. 矩陣中的 PMI 是什麼？

在矩陣中，PMI 是基於矩陣證明陳述的概念。

3. 什麼是數學歸納法？

一個利用基於既定原理的步驟來證明數學陳述的過程。

4. 數學歸納法中的歸納假設是什麼？

PMI 中的第二步，即假設步驟，稱為歸納假設

5. 弱歸納法和強歸納法有什麼區別？

在弱歸納法中，我們假設任何在 A(x) 步驟中為真的陳述，而在強歸納法中，給定的陳述 A(n) 從基礎到 A(x) 步驟的所有步驟都為真。