平行線及其角的關係

---

引言

平行線是指在任何點都不會相交的線，兩條線之間的距離相同。在幾何學中，直線可以是相交線或不相交線。相交線彼此形成一個角，而不相交線彼此不形成任何角。平行線是不相交的線。平行線上的每個點與其在另一條線上對應的點等距。相交線在彼此之間形成 0 度到 360 度的角。在二維平面上，兩條或多條線在幾何學中可以相交、平行和垂直。線可以定義為垂直、平行、橫截等。在本教程中，我們將瞭解平行線、橫截線、平行線和橫截線形成的角、同位角、內錯角和外錯角。我們還將學習關於橫截線同側的角以及一些關於這些主題的解題示例。

平行線

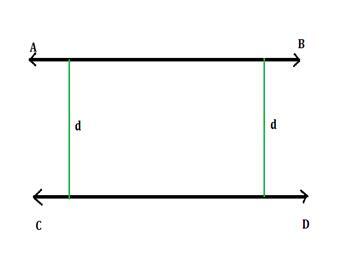
如果二維平面上的兩條線即使延伸到無限遠也不會相交，則這些線稱為共面線或平行線。換句話說，如果這些線上的每個點與其在該平面上對應的點等距，則稱這些線為平行線。

橫截線

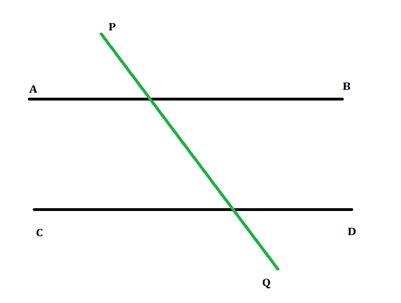
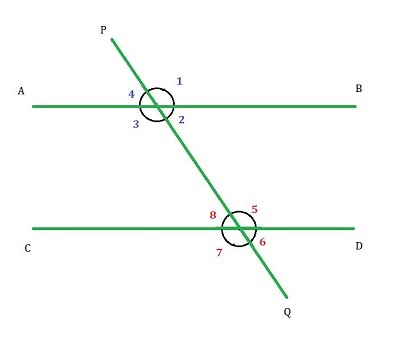
如果二維平面上的兩條平行線被第三條線在兩個不同的點處相交，則第三條線稱為橫截線。如圖所示，橫截線 PQ 在兩個點處與線 AB 和 CD 相交。橫截線與每條線形成八個不同的角，我們將在後面進一步討論。

平行線和橫截線形成的角

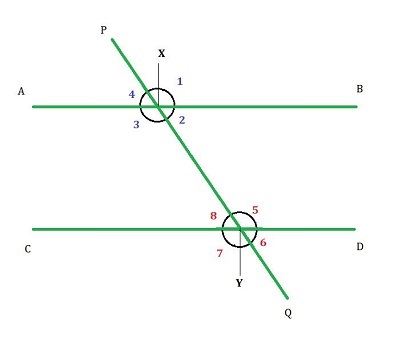
考慮下圖。在圖中，線 AB 平行於線 CD，橫截線 PQ 穿過平行線。橫截線在 X 點與線 AB 相交，在 Y 點與線 CD 相交。如圖所示，橫截線與線 AB 和 CD 形成八個角。這些角彼此之間存在一些關係，這有助於我們確定線之間的角。

橫截線形成的不同型別的角將在後面討論。

同位角

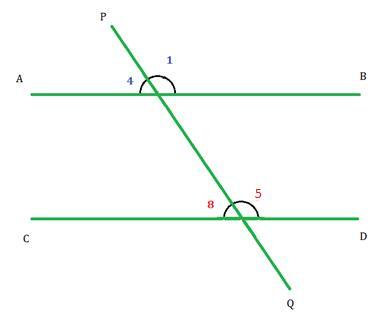
橫截線在第一條線上形成的外角和橫截線在第二條線上形成的內角在橫截線的同一側被稱為同位角。在下圖中，$\mathrm{\angle1}$ 是 $\mathrm{\angle5}$ 的同位角，$\mathrm{\angle4}$ 是 $\mathrm{\angle8}$ 的同位角。並且平行線形成的同位角彼此相等；因此，

$$\mathrm{\angle1\:=\:\angle5}$$

$$\mathrm{\angle4\:=\:\angle8}$$

類似地，橫截線在第一條線上形成的內角和橫截線在第二條線上形成的外角在橫截線的同一側被稱為同位角。

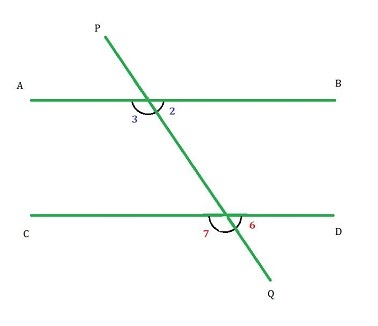
因此，$\mathrm{\angle2\:=\:\angle6}$

$\mathrm{\angle3\:=\:\angle7}$

內錯角和外錯角

與同位角相反，內錯角和外錯角包括橫截線兩側的內角和外角。

內錯角

橫截線在兩條平行線上形成的位於橫截線異側的內角稱為內錯角。如圖所示，$\mathrm{\angle2}$ 是 $\mathrm{\angle8}$ 的內錯角，$\mathrm{\angle3}$ 是 $\mathrm{\angle5}$ 的內錯角。

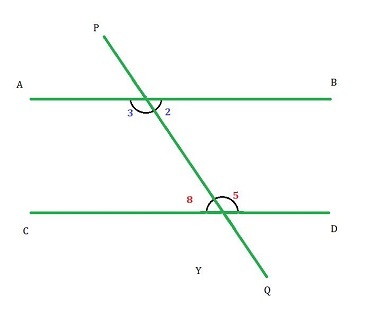
平行線形成的內錯角相等。

因此，$\mathrm{\angle2\:=\:\angle8}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\angle3\:=\:\angle5}$

外錯角

橫截線在其任一側形成的外角稱為外錯角。如圖所示，$\mathrm{\angle1}$ 是 $\mathrm{\angle7}$ 的外錯角，$\mathrm{\angle4}$ 是 $\mathrm{\angle6}$ 的外錯角。

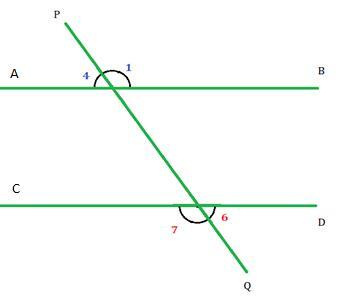
平行線形成的外錯角相等。

因此， $\mathrm{\angle1\:=\:\angle7}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\angle4\:=\:\angle6}$

橫截線同側的角

橫截線在兩條平行線上形成的位於橫截線同側的內角稱為同旁內角。如圖所示，$\mathrm{\angle2}$ 是 $\mathrm{\angle5}$ 的同旁內角，$\mathrm{\angle3}$ 是 $\mathrm{\angle8}$ 的同旁內角。

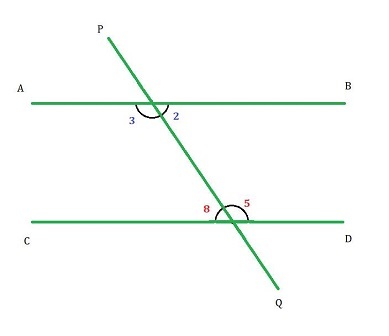
如果一條橫截線與兩條平行線相交，則每對同旁內角互補。

因此， $\mathrm{\angle2\:+\:\angle5\:=\:180°\:\:\:\:\angle3\:+\:\angle8\:=\:180°}$

對頂角

橫截線與兩條平行線在兩個不同點相交形成的每個角與其在同一條線上異側的對角互為對頂角。如圖所示，$\mathrm{\angle1}$ 與同一條線上的 $\mathrm{\angle3}$ 互為對頂角，同樣，$\mathrm{\angle2}$ 和 $\mathrm{\angle4}$，$\mathrm{\angle5}$ 和 $\mathrm{\angle7}$，以及 $\mathrm{\angle6}$ 和 $\mathrm{\angle8}$ 互為對頂角。

對頂角彼此相等。

因此， $\mathrm{\angle1\:=\:\angle3\:,\:\angle2\:=\:\angle4\:,\:\angle5\:=\:\angle7\:,\:\angle6\:=\:\angle8}$

解題示例

1) 在下圖中，線 AB 平行於線 CD。橫截線 PQ 在 X 和 Y 點與線相交。如果 $\mathrm{\angle\:AXP\:=\:60°}$，則求角 $\mathrm{\angle\:PYD}$。

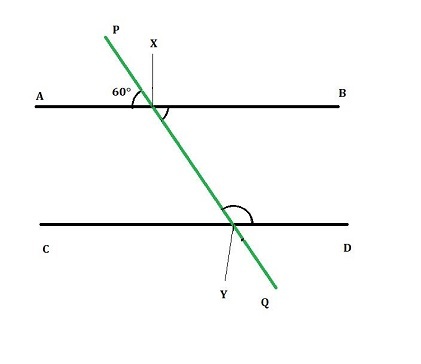
答 - 已知，$\mathrm{\angle\:AXP\:=\:60°\:,\:AB\:\:\:\rVert\:\:CD}$

根據橫截線的性質，對頂角彼此相等。因此，

$$\mathrm{\angle\:AXP\:=\:\angle\:QXB}$$

$$\mathrm{\angle\:QXB\:=\:60°}$$

根據橫截線同側角的性質，

$$\mathrm{\angle\:QXB\:+\:\angle\:PYD\:=\:180°}$$

$$\mathrm{60°\:+\:\angle\:=\:180°}$$

$$\mathrm{\angle\:PYD\:=\:120°}$$

2) 在給定圖中求 x，其中線 AB 和 CD 是平行線，PQ 是穿過它們的橫截線。已知，$\mathrm{\angle\:QXB\:=\:72°}$

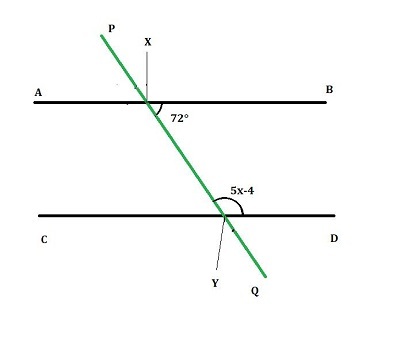
答 - 已知 $\mathrm{\angle\:QXB\:=\:72°\:,\:AB\:\:\:\rvert\:\:\:CD\:,\:\angle\:PYD\:=\:5x\:-\:4}$

根據橫截線同側內角的性質，

$$\mathrm{\angle\:QXB\:+\:\angle\:PYD\:=\:180°}$$

$$\mathrm{72°\:+\:5x\:-\:4\:=\:180°}$$

$$\mathrm{5x\:-\:4\:=\:108°}$$

$$\mathrm{5x\:=\:112°}$$

$$\mathrm{x\:=\:224°}$$

結論

線可以定義為垂直、平行、橫截等。平行線是不相交的線。平行線上的每個點與其在另一條線上對應的點等距。如果二維平面上的兩條平行線被第三條線在兩個不同的點處相交，則第三條線稱為橫截線。橫截線在第一條線上形成的外/內角和橫截線在第二條線上形成的內/外角在橫截線的同一側被稱為同位角。橫截線在兩條平行線上形成的位於橫截線異側的內/外角稱為內錯角/外錯角。當橫截線與其中一條平行線相交時，彼此相對的角稱為對頂角。

常見問題

1. 橫截線穿過兩條平行線時會形成多少個角？

橫截線穿過兩條平行線時會形成八個角。

2. 什麼是同位角？

橫截線在第一條線上形成的外/內角和橫截線在第二條線上形成的內/外角在橫截線的同一側被稱為同位角。

3. 內角之間是什麼關係？

橫截線同側的內角互補，即它們的和等於 180°。橫截線異側的內角相等。

4. 什麼是對頂角？

當橫截線與其中一條平行線相交時，彼此相對的角稱為對頂角。

5. 什麼是內錯角和外錯角？

橫截線在兩條平行線上形成的位於橫截線異側的內角稱為內錯角。