資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學藉助圖表，推匯出以下關係
a. 速度-時間
b. 位置-時間
c. 位置-速度（推匯出三個運動方程）
速度-時間
一輛初始速度為u的汽車，在一段時間t內受到均勻加速度a的作用，t時間後汽車的最終速度為v。
現在我們需要用圖形方法找到v、u、a、t之間的關係。
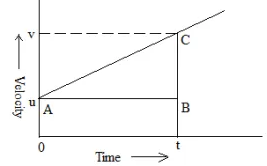
A點處的初始速度u = OA
最終速度為V
速度-時間圖的斜率等於加速度a。
$a\ =\ \frac{v\ -\ u}{t\ -\ 0}$
$\Longrightarrow \ v\ =\ u\ +\ at$
位置-時間
考慮一個具有初始速度u的物體的線性運動。假設物體均勻加速，並在時間t後獲得最終速度v。速度-時間圖是一條直線AB，如下所示。
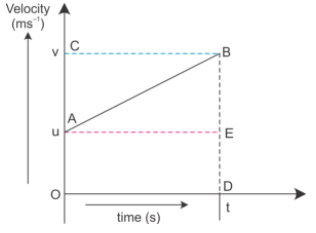
當t = 0時，初始速度 = u = OA
當t = t時，最終速度 = v = OC
時間t內行駛的距離S = 梯形OABD的面積
$s\ =\ \frac{1}{2} \ \times \ ( OA\ +\ DB) \ \times \ OD$
$s\ =\ \frac{1}{2} \ \times \ ( u\ +\ v) \ \times \ t$
由於v = u + at，
$s\ =\ \frac{1}{2} \ \times \ ( u+\ u\ +\ at) \ \times \ t$
$s\ =\ ut\ +\ \frac{1}{2} at^{2}$
速度-位置
從速度-時間關係式
$t\ =\ \frac{v\ -\ u}{a}$
將't'的值代入方程$s\ =\ \frac{1}{2} \ \times \ ( u\ +\ v) \ \times \ t$
我們得到：
$s\ =\ \left(\frac{v\ +\ u}{2}\right) \ \times \ \left(\frac{v\ -\ u}{2}\right)$
=> v²=u²+2as
47 次瀏覽
