群速度和相速度之間的關係

---

簡介

在本教程中，將討論有關波的特性（例如相速度和群速度）的資訊，並輔以適當的示例。在物理學中，波可以定義為在平面表面上識別的單純擾動。

基於此概念，本教程將討論群速度和相速度的定義。此外，本教程還將包括這兩個波特性之間共享的關係和差異。

什麼是群速度？

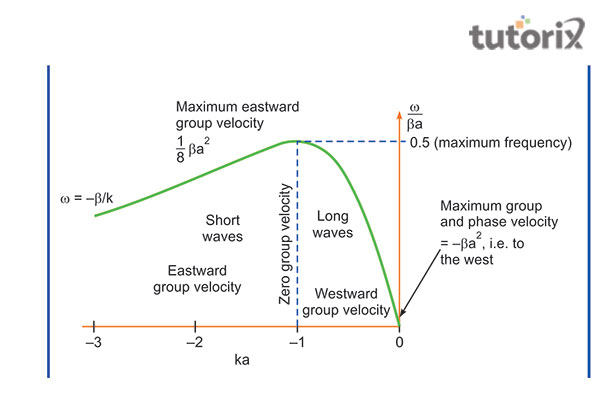
圖 1：群速度

波的群速度可以解釋為在空間中傳播時表現出波振幅的整體包絡形狀的速度。根據量子物理學的術語，透過具有不同振幅和數量的不同波獲得“波包”（Sciencedirect，2022）。

• 該粒子的速度被認為等同於發展“波包”的波群。

• 波群的速度由數學表示式“v_g= dω/dk”表示，它表示粒子運動的速度。

相速度的定義

圖 2：相速度

波在穿過光譜或任何波包時其相位的速度。例如，可以根據上圖得出，其中波的 A 點以“相速度”傳播，可以用數學表示為“v_p=ωk”（Jin & Gaherty，2019）。

為了建立這種數學表示，考慮角頻率也很重要，它由“ω = 2π f”表示。此方程與角波數相關，角波數由“k = 2π / λ”表示，其中頻率和波長分別由 f 和 λ 表示。

相速度和群速度之間的差異

在“反常”介質中，相速度低於“群速度”，而如果波穿過正常介質，則“相速度”的值大於“群速度”。在用波表示粒子的情況下，“群速度”具有更大的重要性，而在處理單個波時，“相速度”具有這種重要性（Yu et al. 2019）。

然而，在“波包”中，已經觀察到包絡以“波群”的速度傳播。相反，已經觀察到載波以“相速度”在波包中傳播。基於這些矛盾，這兩個波分量的數學公式也不同。群速度的公式為“v_g= dω/dk = v_p+ k dv_p / dk”，而相速度的公式為“v_p= ωk = λf”。

群速度和相速度之間的關係

圖 3：相速度和群速度之間的關係

“相速度”和“群速度”之間共享的關係指出，被認為是群速度的一組波的速度與這些波的“相速度”成“正比”。這種關係揭示了“相速度”和“群速度”之間的直接關係（Kondakci & Abouraddy，2019）。

基於這種關係，可以認為波的這兩個分量相互依賴。

例如，可以說當波群的速度增加時，相速度的值將以相同的速率增加。另一方面，群速度的值將根據“相速度”的減小值而減小。

相速度和群速度之間的數學關係

“群速度”和“相速度”之間的數學關係如下：

為了獲得波包的振幅，假設 ω 被認為是角速度，由“ω = 2πf”給出。K 代表角波數，由“k = 2π / λ”給出，字母 t 和 x 分別表示時間和位置。根據第一個方程“ω = kV_p”，k 的值為“dw / dk = V_p + k (dV_p/dk)”。基於此，獲得的方程為“V_g = V_p + k (dV_p/dk)”，它顯示了相速度和群速度之間的直接關係。

結論

本教程闡明瞭波的“群速度”的概念。此外，“相速度”被解釋為波在任何介質中“傳播”的速率。本教程包含了這兩個“波的特性”之間的核心差異，並指出在“正常介質”中，“相速度”比“群速度”高。這兩個特性之間形成的關係是這兩個波的特性“彼此成正比”。

常見問題

Q1. 在“相速度”的上下文中，定義“色散”和“非色散正弦波”。

答：在色散波的情況下，指的是“相速度”，波的速度和速度在功能上是不同的，而在“非色散波”中，頻率不同，但“不同波”的速度是統一的。

Q2. “相速度”和“波速”相同嗎？

答：一般來說，如果概念中沒有提出任何規範，波速通常稱為相速度，因為它解釋了相位在空間中傳播時保持的特定速率。

Q3. 群速度在物理學中的作用是什麼？

答：群速度的值有助於確定“波包傳播”能量的速度。在“量子力學”中，運動粒子的位置的期望值由群速度理解。

Q4. 在什麼情況下相速度和群速度相等？

答：在兩個“單色波”穿過真空傳播的情況下，這兩個波的相速度變得相似，並且“疊加波”的相速度等同於“群速度”。