從下面給出的選項中，選擇其影像在圖 4.6 和圖 4.7 中所示的方程。
對於圖 4.6

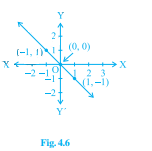
(i) \( y=x \)
(ii) \( x+y=0 \)
(iii) \( y=2 x \)
(iv) \( 2+3 y=7 x \)
對於圖 4.7


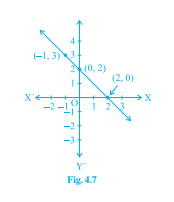
(i) \( y=x+2 \)
(ii) \( y=x-2 \)
(iii) \( y=-x+2 \)
(iv) \( x+2 y=6 \)

題目：

我們必須找到圖4.6和圖4.7中所示的方程。

解答

對於圖 4.6

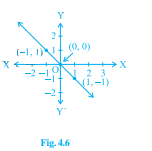
讓我們將給定的點代入選項中的每個方程。

給定的點應該滿足圖中所示方程。

因此，

(i) (-1, 1)

\(y=x\)

\(-1≠1\)

(ii) (-1, 1)

\(x+y=0\)

$-1+1=0$

$0+0=0$

$1-1=0$

因此，(-1, 1) 和 (1, -1) 滿足方程 \(x+y=0\)。

(iii) (-1, 1)

\(y=2x\)

$1=2(-1)$

\(1≠-2\)

(iv) (-1, 1)

\(2+3y=7x\)

$2+3(1)=7(-1)$

$2+3=-7$

\(5≠-7\)

因此，圖 4.6 中所示的方程是 \(x+y=0\)。 

對於圖 4.7

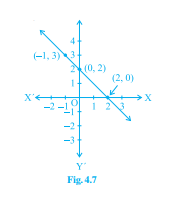
讓我們將給定的點代入選項中的每個方程。

給定的點應該滿足圖中所示方程。

因此，

(i) (-1, 3)

\(y=x+2\)

\(3≠-1+2\)

(ii) (-1, 3)

\(y=x-2\)

\(3≠-1-2\)

(iii) (-1, 3)

\(y=-x+2\)

\(-x+2=-(-1)+2\)

$=1+2$

$=3$

$(2, 0)$

\(y=-x+2\)

\(-x+2=3\)

$=0$

\(=y\)

因此，(-1, 3) 和 (2, 0) 滿足方程 \(y=-x+2\)。

(iv) (-1, 3)

\(x+2y=6\)

\(x+2y=-1+2(3)\)

$=-1+6$

$=5$

\(≠6\)

因此，圖 4.7 中所示的方程是 \(y=-x+2\)。 

教程點

更新於：2022年10月10日

33 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習