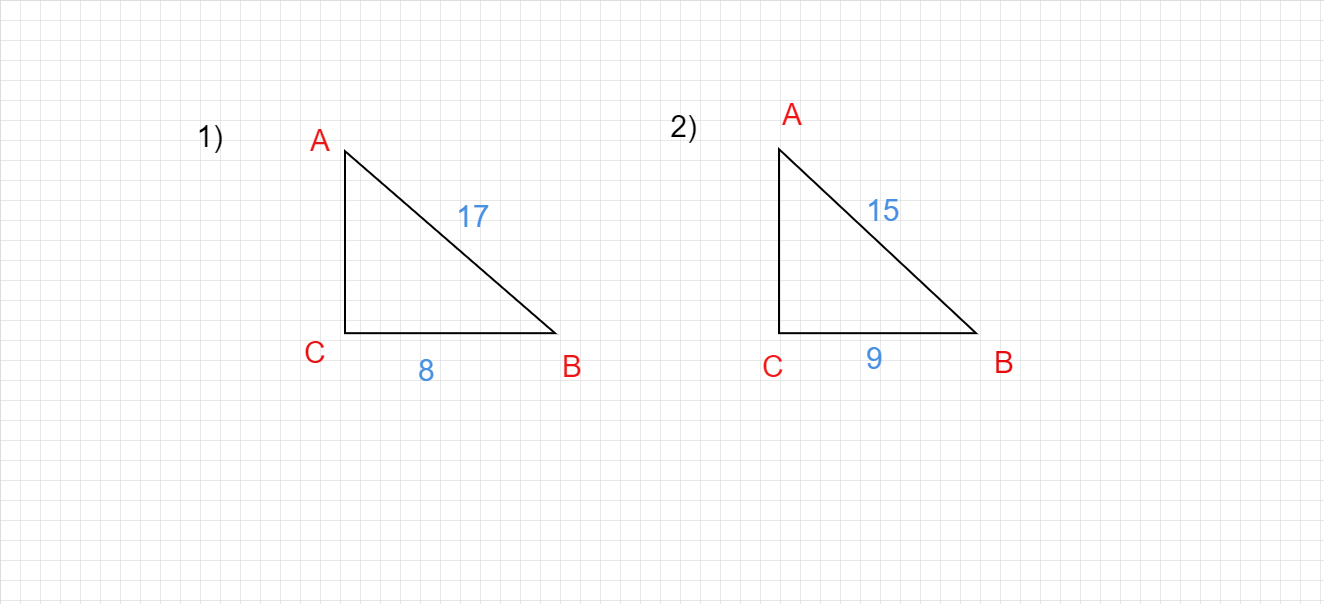
在下面的圖形中找到垂直邊的未知值
"\n

已知

給出直角三角形。

要求

我們必須找到三角形的未知垂直邊。

解

勾股定理是直角三角形三邊之間的一種基本關係。

它指出，以斜邊為邊的正方形的面積等於另外兩邊上的正方形面積之和。(h^2= a^2+ b^2)。

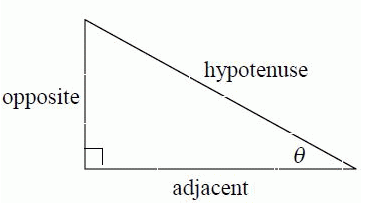
$h^2= a^2 + b^2$

其中 h 是斜邊，a、b 是直角三角形的另外兩邊。

(1) $AB^2= AC^2+ BC^2$   

$17^2= AC^2+ 8^2$ 

$289 = AC^2+ 64$

$AC^2 = 289-64$

$AC^2 = 225$

$AC^2= 15 \times 15$

AC = 15。

因此，垂直邊為 15。

(2)$AB^2= AC^2+ BC^2$ 

$15^2= AC^2+ 9^2$ 

$225 = AC^2+ 81$

$AC^2 = 225-81$

$AC^2 = 144$

$AC^2= 12 \times 12$

AC = 12。

因此，垂直邊為 12。

Tutorialspoint

更新時間： 2022年10月10日

38 次瀏覽

開啟你的 職業生涯

完成課程獲得認證

開始學習