資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
服裝研究
法律研究畫出下列度數的角
(i) \( 30^{\circ} \)
(ii) \( 22 \frac{1}{2} \)
(iii) \( 15^{\circ} \).
步驟
我們需要畫出給定的角度。
解
(i)
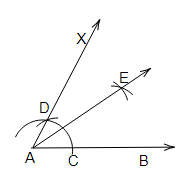
作圖步驟
(a) 畫一條射線 $AB$。
(b) 以 $A$ 為圓心，適當的半徑畫弧，交 $AB$ 於 $C$。
(c) 以 $C$ 為圓心，與上述相同的半徑畫弧，交之前的弧於 $D$。
(d) 延長 $AD$，形成射線 $AX$
因此，
$\angle BAX= 60^o$。
(e) 以 $C$ 和 $D$ 為圓心，半徑大於 $\frac{1}{2}CD$ 畫兩弧，交於 $E$。
(f) 連線 $A$ 和 $E$ 並延長形成射線 $AE$。
因此，$BAE=30^o$
(ii)
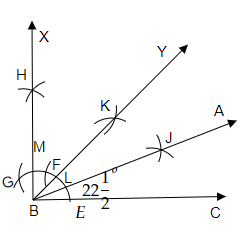
作圖步驟
(a) 畫一條射線 $BC$。
(b) 以 $B$ 為圓心，適當的半徑畫弧，交 $BC$ 於 $E$。
(c) 以 $E$ 為圓心，與上述相同的半徑畫弧，交之前的弧於 $F$。
(d) 以 $F$ 為圓心，與上述相同的半徑畫弧，交第一條弧於 $G$。
(c) 以 $F$ 和 $G$ 為圓心，半徑大於 $\frac{1}{2}FG$ 畫兩弧，交於 $H$。
(d) 連線 $BH$
$\angle HBC = 90^o$。
(e) 令 $BH$ 交第一條弧於 $M$。
(f) 以 $E$ 和 $M$ 為圓心，半徑大於 $\frac{1}{2}EM$ 畫兩弧，交於 $K$。
(g) 連線 $B$ 和 $K$ 並延長形成射線 $BY$
$\angle CBK=45^o$
(h) 令 $L$ 為射線 $BY$ 與第一條弧的交點。
(i) 以 $E$ 和 $L$ 為圓心，半徑大於 $\frac{1}{2}EL$ 畫兩弧，交於 $J$。
(j) 連線 $LJ$ 並延長形成射線 $BA$
(k) 因此，$\angle CBA=22\frac{1}{2}^o$
(iii)
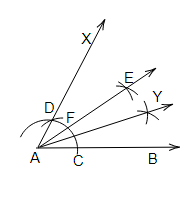
作圖步驟
(a) 畫一條射線 $AB$。
(b) 以 $A$ 為圓心，適當的半徑畫弧，交 $AB$ 於 $C$。
(c) 以 $C$ 為圓心，與上述相同的半徑畫弧，交之前的弧於 $D$。
(d) 延長 $AD$，形成射線 $AX$
因此，
$\angle BAX= 60^o$。
(e) 以 $C$ 和 $D$ 為圓心，半徑大於 $\frac{1}{2}CD$ 畫兩弧，交於 $E$。
(f) 連線 $A$ 和 $E$ 並延長形成射線 $AE$。
因此，$BAE=30^o$
(g) 令 $F$ 為射線 $AE$ 與第一條弧的交點。
(h) 以 $C$ 和 $F$ 為圓心，半徑大於 $\frac{1}{2}CF$ 畫兩弧，交於 $Y$。
(i) 連線 $AY$
因此，$BAY=15^o$。
30 次瀏覽
