CNTK - 迴圈神經網路

上一頁
下一頁

現在，讓我們瞭解如何在 CNTK 中構建迴圈神經網路 (RNN)。

簡介

我們學習瞭如何使用神經網路對影像進行分類，這是深度學習中一項標誌性的工作。但是，神經網路擅長的另一個領域以及正在進行的大量研究是迴圈神經網路 (RNN)。在這裡，我們將瞭解什麼是 RNN 以及如何在需要處理時間序列資料的情況下使用它。

什麼是迴圈神經網路？

迴圈神經網路 (RNN) 可以定義為能夠進行時間推理的特殊神經網路。RNN 主要用於需要處理隨時間變化的值（即時間序列資料）的場景。為了更好地理解它，讓我們比較一下常規神經網路和迴圈神經網路：

  • 眾所周知，在常規神經網路中，我們只能提供一個輸入。這限制了它只能產生一個預測結果。舉個例子，我們可以使用常規神經網路來完成文字翻譯工作。

  • 另一方面，在迴圈神經網路中，我們可以提供一系列樣本，從而產生單個預測。換句話說，使用 RNN，我們可以根據輸入序列預測輸出序列。例如，在翻譯任務中，RNN 進行了一些相當成功的實驗。

迴圈神經網路的用途

RNN 可以以多種方式使用。其中一些如下所示：

預測單個輸出

在深入探討 RNN 如何根據序列預測單個輸出的步驟之前，讓我們看看基本的 RNN 是什麼樣子：

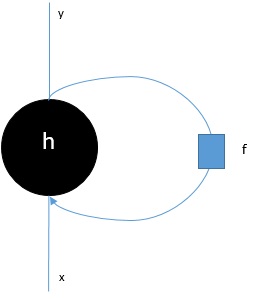
Single Output

如上圖所示，RNN 包含一個迴環連線到輸入，並且每當我們饋送一系列值時，它都會將序列中的每個元素處理為時間步。

此外，由於迴環連線，RNN 可以將生成的輸出與序列中下一個元素的輸入結合起來。透過這種方式，RNN 將在整個序列上構建一個記憶，該記憶可用於進行預測。

為了使用 RNN 進行預測，我們可以執行以下步驟：

  • 首先，為了建立初始隱藏狀態，我們需要饋送輸入序列的第一個元素。

  • 然後，為了生成更新的隱藏狀態，我們需要獲取初始隱藏狀態並將其與輸入序列中的第二個元素結合起來。

  • 最後，為了生成最終隱藏狀態並預測 RNN 的輸出，我們需要獲取輸入序列中的最後一個元素。

透過這種方式，藉助此迴環連線，我們可以訓練 RNN 識別隨時間發生的模式。

預測序列

上面討論的基本 RNN 模型也可以擴充套件到其他用例。例如，我們可以使用它根據單個輸入預測一系列值。在這種情況下，為了使用 RNN 進行預測，我們可以執行以下步驟：

  • 首先，為了建立初始隱藏狀態並預測輸出序列中的第一個元素，我們需要將輸入樣本饋送到神經網路。

  • 然後，為了生成更新的隱藏狀態和輸出序列中的第二個元素，我們需要將初始隱藏狀態與相同的樣本結合起來。

  • 最後，為了再次更新隱藏狀態並預測輸出序列中的最後一個元素，我們將樣本再次饋送。

預測序列

我們已經瞭解瞭如何根據序列預測單個值以及如何根據單個值預測序列。現在讓我們看看如何為序列預測序列。在這種情況下，為了使用 RNN 進行預測，我們可以執行以下步驟：

  • 首先，為了建立初始隱藏狀態並預測輸出序列中的第一個元素，我們需要獲取輸入序列中的第一個元素。

  • 然後，為了更新隱藏狀態並預測輸出序列中的第二個元素，我們需要獲取初始隱藏狀態。

  • 最後，為了預測輸出序列中的最後一個元素，我們需要獲取更新的隱藏狀態和輸入序列中的最後一個元素。

RNN 的工作原理

要了解迴圈神經網路 (RNN) 的工作原理，我們需要首先了解網路中的迴圈層如何工作。因此，首先讓我們討論如何使用標準迴圈層預測輸出。

使用標準 RNN 層預測輸出

正如我們之前所討論的那樣，RNN 中的基本層與神經網路中的常規層有很大不同。在上一節中，我們還在圖中演示了 RNN 的基本架構。為了更新序列中第一個時間步的隱藏狀態，我們可以使用以下公式：

Rnn Layer

在上述等式中，我們透過計算初始隱藏狀態與一組權重的點積來計算新的隱藏狀態。

現在對於下一步，當前時間步的隱藏狀態用作序列中下一個時間步的初始隱藏狀態。因此，為了更新第二個時間步的隱藏狀態，我們可以重複在第一個時間步中執行的計算，如下所示：

First Step

接下來，我們可以重複更新序列中第三個和最後一個時間步的隱藏狀態的過程，如下所示：

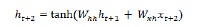
Last Step

當我們處理完序列中的所有上述步驟後，我們可以計算輸出，如下所示：

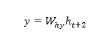
Calculate Output

對於上述公式，我們使用了第三組權重和來自最終時間步的隱藏狀態。

高階迴圈單元

基本迴圈層的主要問題是梯度消失問題，並且由於此問題，它在學習長期相關性方面表現不佳。簡單來說，基本迴圈層不能很好地處理長序列。這就是為什麼其他一些更適合處理更長序列的迴圈層型別如下所示：

長短期記憶 (LSTM)

Long-Short Term Memory (LSTM)

長短期記憶 (LSTM) 網路由 Hochreiter & Schmidhuber 引入。它解決了使基本迴圈層能夠長時間記住事物的問題。LSTM 的架構如上圖所示。我們可以看到它具有輸入神經元、記憶單元和輸出神經元。為了克服梯度消失問題，長短期記憶網路使用顯式記憶單元（儲存先前值）和以下門：

  • 遺忘門 - 顧名思義，它告訴記憶單元忘記先前值。記憶單元儲存值，直到門（即“遺忘門”）告訴它忘記它們。

  • 輸入門 - 顧名思義，它向單元格新增新內容。

  • 輸出門 - 顧名思義，輸出門決定何時將來自單元格的向量傳遞到下一個隱藏狀態。

門控迴圈單元 (GRU)

Gated Recurrent Units (GRUs)

門控迴圈單元 (GRU) 是 LSTM 網路的一個輕微變體。它少了一個門，並且其連線方式與 LSTM 略有不同。其架構如上圖所示。它具有輸入神經元、門控記憶單元和輸出神經元。門控迴圈單元網路具有以下兩個門：

  • 更新門 - 它確定以下兩件事：

    • 應從上一個狀態保留多少資訊？

    • 應從上一層傳入多少資訊？

  • 重置門 - 重置門的功能與 LSTM 網路的遺忘門非常相似。唯一的區別是它位於略微不同的位置。

與長短期記憶網路相比，門控迴圈單元網路速度稍快且更容易執行。

建立 RNN 結構

在我們開始對任何資料來源的輸出進行預測之前，我們需要首先構建 RNN，構建 RNN 與我們在上一節中構建常規神經網路的方式非常相似。以下是構建一個的程式碼：

from cntk.losses import squared_error
from cntk.io import CTFDeserializer, MinibatchSource, INFINITELY_REPEAT, StreamDefs, StreamDef
from cntk.learners import adam
from cntk.logging import ProgressPrinter
from cntk.train import TestConfig
BATCH_SIZE = 14 * 10
EPOCH_SIZE = 12434
EPOCHS = 10

堆疊多層

我們還可以堆疊 CNTK 中的多個迴圈層。例如，我們可以使用以下層的組合：

from cntk import sequence, default_options, input_variable
from cntk.layers import Recurrence, LSTM, Dropout, Dense, Sequential, Fold
features = sequence.input_variable(1)
with default_options(initial_state = 0.1):
   model = Sequential([
      Fold(LSTM(15)),
      Dense(1)
   ])(features)
target = input_variable(1, dynamic_axes=model.dynamic_axes)

如上程式碼所示，我們在 CNTK 中對 RNN 建模有以下兩種方式：

  • 首先，如果我們只需要迴圈層的最終輸出，我們可以將Fold層與迴圈層（如 GRU、LSTM 或甚至 RNNStep）結合使用。

  • 其次，作為替代方法，我們還可以使用Recurrence塊。

使用時間序列資料訓練 RNN

構建模型後，讓我們看看如何在 CNTK 中訓練 RNN：

from cntk import Function
@Function
def criterion_factory(z, t):
   loss = squared_error(z, t)
   metric = squared_error(z, t)
   return loss, metric
loss = criterion_factory(model, target)
learner = adam(model.parameters, lr=0.005, momentum=0.9)

現在，要將資料載入到訓練過程中，我們必須從一組 CTF 檔案中反序列化序列。以下程式碼包含create_datasource函式，這是一個用於建立訓練和測試資料來源的有用實用函式。

target_stream = StreamDef(field='target', shape=1, is_sparse=False)
features_stream = StreamDef(field='features', shape=1, is_sparse=False)
deserializer = CTFDeserializer(filename, StreamDefs(features=features_stream, target=target_stream))
   datasource = MinibatchSource(deserializer, randomize=True, max_sweeps=sweeps)
return datasource
train_datasource = create_datasource('Training data filename.ctf')#we need to provide the location of training file we created from our dataset.
test_datasource = create_datasource('Test filename.ctf', sweeps=1) #we need to provide the location of testing file we created from our dataset.

現在，由於我們已經設定了資料來源、模型和損失函式，我們可以開始訓練過程。這與我們在前面使用基本神經網路的章節中所做的方法非常相似。

progress_writer = ProgressPrinter(0)
test_config = TestConfig(test_datasource)
input_map = {
   features: train_datasource.streams.features,
   target: train_datasource.streams.target
}
history = loss.train(
   train_datasource,
   epoch_size=EPOCH_SIZE,
   parameter_learners=[learner],
   model_inputs_to_streams=input_map,
   callbacks=[progress_writer, test_config],
   minibatch_size=BATCH_SIZE,
   max_epochs=EPOCHS
)

我們將獲得類似以下的輸出：

輸出：

average  since  average  since  examples
loss      last  metric  last
------------------------------------------------------
Learning rate per minibatch: 0.005
0.4      0.4    0.4      0.4      19
0.4      0.4    0.4      0.4      59
0.452    0.495  0.452    0.495   129
[…]

驗證模型

實際上，使用 RNN 進行預測與使用任何其他 CNK 模型進行預測非常相似。唯一的區別是我們需要提供序列而不是單個樣本。

現在，由於我們的 RNN 最終完成了訓練，我們可以透過使用一些樣本序列對其進行測試來驗證模型，如下所示：

import pickle
with open('test_samples.pkl', 'rb') as test_file:
test_samples = pickle.load(test_file)
model(test_samples) * NORMALIZE

輸出：

array([[ 8081.7905],
[16597.693 ],
[13335.17 ],
...,
[11275.804 ],
[15621.697 ],
[16875.555 ]], dtype=float32)
列印頁面

上一頁
下一頁
廣告