阿伏伽德羅原子尺寸測量

---

引言

許多科學家都在嘗試測量原子的尺寸。但阿伏伽德羅假說對此做出了重要的解釋。阿伏伽德羅假說是在阿伏伽德羅去世兩年後才被接受的。義大利化學家斯坦尼斯勞·坎尼扎羅能夠解釋化學中阿伏伽德羅假說的例外情況後，該假說才被接受。他解釋並證明了原子、分子與各種物質重量之間的關係。

現在，我們將討論阿伏伽德羅假說，並學習如何使用阿伏伽德羅定律計算原子的大小。

阿伏伽德羅是誰？

阿梅代奧·阿伏伽德羅，全名洛倫佐·羅馬諾·阿梅代奧·卡洛·阿伏伽德羅（1776年8月9日出生，1856年7月9日去世），是一位義大利科學家。他以對氣體體積(V)、壓力(P)和溫度(T)的研究而聞名。他推匯出了被稱為阿伏伽德羅定律或阿伏伽德羅假說的氣體定律。對於原子理論的研究，阿伏伽德羅被認為是早期的人物，並且至今仍是重要的貢獻者。

他學習教會法並自行執業。之後，阿伏伽德羅開始自學物理和數學兩門學科。他和他的兄弟一起進行了第一次物理實驗。

之後，他開始教學，期間他進行氣體密度實驗。他成為都靈大學數學物理學的第一任教授。他的主要貢獻是澄清了原子和分子之間的混淆。為了紀念阿伏伽德羅，一摩爾物質中的分子數量被稱為阿伏伽德羅數，也稱為阿伏伽德羅常數。每摩爾克的分子實驗值為$\mathrm{6.023\:\times10^{23}}$

阿伏伽德羅假說

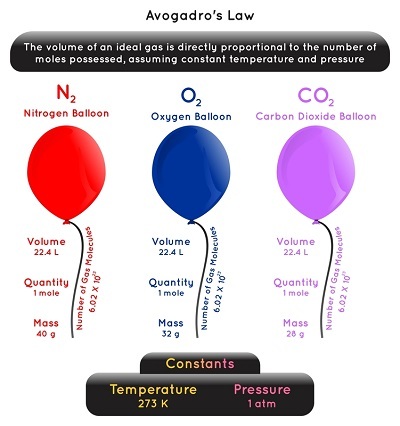
阿伏伽德羅假說也稱為阿伏伽德羅原理或阿伏伽德羅定律。

它指出，在恆溫恆壓條件下，氣體的原子或分子總數與其佔據的體積成正比。

現在，如果我們取兩種理想氣體，並等量混合，那麼它們包含相同數量的分子。如果氣體（表現出理想行為）保持相同的壓力和溫度，這是可能的。因此，我們可以用數學公式寫成：

$$\mathrm{V\:\varpropto\:n}$$

或者我們可以寫成：

$$\mathrm{\frac{V}{n}\:=\:k}$$

其中，V - 氣體體積

n - 氣態物質，K - 特定壓力和溫度下的常數 在不同條件下，如果比較同一種氣態物質

$$\mathrm{\frac{V_{1}}{n_{1}}\:=\frac{V_{2}}{n_{2}}}$$

因此，從上式可以看出，氣體體積增加，氣體摩爾數也增加。減少的情況也是如此。因此，在特定體積的氣體中，存在的分子或原子總數與氣體的摩爾質量無關。

阿伏伽德羅數

阿伏伽德羅數定義為：在一摩爾物質（其分子量以克為單位測量）中，單元數等於$\mathrm{6.023\:\times10^{23}}$

對於輕氣體和重氣體，考慮因素相同。我們討論的單元可以是電子、離子、原子或分子，這取決於材料的性質和反應的任何傾向。

阿伏伽德羅假說如何幫助確定原子的尺寸？

利用阿伏伽德羅假說，我們可以計算出原子的半徑。設物質摩爾質量為‘M’，原子數為N，

$$\mathrm{每克原子數\:=\:\frac{N}{M}}$$

$$\mathrm{每克原子的總體積\:=\:\frac{N}{M}\:\times\frac{4}{3}\:\Pi\:r^{3}}$$

根據阿伏伽德羅假說，一克物質中原子的實際體積是該克物質體積的三分之二。

$$\mathrm{\:\frac{N}{M}\:\times\frac{4}{3}\:\Pi\:r^{3}\:=\:\frac{2}{3}v}$$

{{我們知道密度，$\mathrm{\rho\:=\:\frac{質量}{體積}\:=\:\frac{1}{v}}$}}

因此，$\mathrm{\:\frac{N}{M}\:\times\frac{4}{3}\:\Pi\:r^{3}\:=\:\frac{2}{3\rho}}$

$$\mathrm{r^{3}\:=\:\frac{2\:\times\:3M}{3\rho\pi4N}\:=\:\frac{M}{2\pi\:N\rho}}$$

$$\mathrm{r\:=[\:\frac{M}{2\pi\:N\rho\:}]^{\frac{1}{3}}}$$

因此，根據這個公式，我們可以很容易地計算出原子的半徑，從而計算出原子的尺寸。

例題 -

例1：飛輪中20升體積容納10摩爾空氣。但有時飛輪會損失50升體積。求飛輪漏氣量。（假設溫度和壓力保持恆定）

解：已知，初始空氣量，𝑛1 $\mathrm{n_{1}\:=\:10\:mol}$

飛輪的初始體積，$\mathrm{v_{1}\:=\:20\:L}$

飛輪的最終體積，$\mathrm{v_{2}\:=\:50\:L}$

根據阿伏伽德羅定律

$$\mathrm{\frac{v_{1}}{n_{1}}\:=\:\frac{v_{2}}{n_{2}}}$$

$$\mathrm{n_{2}\:=\:\frac{v_{2}}{v_{1}}\:\times\:n_{1}}$$

$$\mathrm{n_{2}\:=\:\frac{50}{20}\:\times\:10}$$

$$\mathrm{n_{2}\:=25\:mol}$$

因此，飛輪漏氣量為25摩爾。

例2：一個氣球最初充入2摩爾氫氣，體積為2.5升。如果再加入2摩爾氫氣，氣球的體積是多少？考慮壓力和溫度保持恆定。

解：已知，初始氣體量 $\mathrm{n_{1}\:=2\:mol}$

氣球的初始體積，$\mathrm{v_{1}\:=2.5\:L}$

最終氣體量，$\mathrm{n_{2}\:=2\:+\:2\:=\:4\:mol}$

根據阿伏伽德羅定律

$$\mathrm{v_{2}\:=\frac{V_{1}}{N_{1}}\:\times\:n_{2}}$$

$$\mathrm{v_{2}\:=\frac{2.5}{2}\:\times\:4\:=\:5\:升}$$

因此，氣球的新體積為5升。

結論

分子一詞源於摩爾一詞。阿伏伽德羅定律可以確定氣體量 (n) 如何與其體積 (v) 相關。發現它是一種直接關係，這表明氣體體積與其存在的摩爾數成正比。這表明一摩爾中含有6.023 × 10²³個分子。

阿伏伽德羅無法確定關於雙原子分子特徵的假設。利用這個假設，我們可以根據在一定溫度和壓力下組合氣體體積來推斷各種氣體物質的化學式和原子的尺寸。

在本教程中，我們介紹了阿伏伽德羅假說、阿伏伽德羅定律、原子尺寸的測量以及阿伏伽德羅假說的侷限性。

常見問題

1. 描述6.023 × 10²³個特徵粒子的術語是什麼？

摩爾質量是描述6.023 × 10²³個特徵粒子的術語。

2. 寫出阿伏伽德羅定律的一些應用？

阿伏伽德羅定律的一些應用包括：

• 它有助於確定氣體的原子性。

• 給出了分子量和蒸氣密度之間的關係。

• 解釋蓋-呂薩克定律。

• 它有助於確定氣體的分子式。

3. 如果在恆溫下給定氣體的體積變為原來的3倍，則壓力是多少？如果‘p’是氣體的初始壓力？

根據玻意耳定律

$$\mathrm{P_{1}\:V_{1}\:=\:P_{2}\:V_{2}}$$

$$\mathrm{\rho\:V_{1}\:=\:P_{2}\:3V_{1}}$$

$$\mathrm{P_{2}\:=\:\frac{\rho}{3}}$$

因此，壓力變為$\mathrm{\frac{\rho}{3}}$

4. 阿伏伽德羅定律的侷限性是什麼？

它只適用於較輕的分子（如氫氣或氦氣）。因為它只適用於真實氣體。儘管它適用於理想氣體，但這導致了該定律的侷限性。

5. 氣體常數的其他名稱是什麼？

氣體常數也稱為理想氣體常數、普適氣體常數或摩爾氣體常數。