
Matlab矩陣 - 快速指南
Matlab矩陣 - 簡介
MATLAB(矩陣實驗室)是一種第四代高階程式語言和互動式環境,用於數值計算、視覺化和程式設計。它允許進行矩陣操作;函式和資料的繪圖;演算法的實現;使用者介面的建立;與用其他語言編寫的程式(包括 C、C++、Java 和 FORTRAN)的介面;分析資料;開發演算法;以及建立模型和應用程式。
在本教程中,我們將重點介紹使用 MATLAB 實現矩陣。
矩陣
矩陣是由按行和列排列的數字組成的集合,表示一個矩形陣列。
下面顯示了一個具有 2 行 3 列的矩陣示例
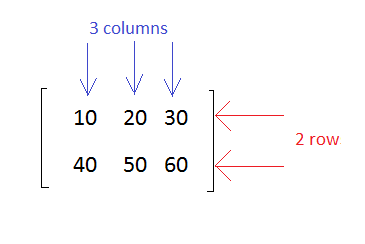
矩陣維度
矩陣的維度根據行數和列數定義。
具有 2 行 3 列的矩陣稱為 2x3 矩陣。
具有 3 行 3 列的矩陣稱為 3x3 矩陣。
Matlab中的矩陣
在 MATLAB 中,您可以透過輸入每一行中以逗號或空格分隔的數字,並使用分號標記每一行的結束來建立矩陣。
示例
要建立一個 4x5 矩陣,請輸入以下內容。
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]
該矩陣有 4 行 5 列。
第一行將具有 1 2 3 4 5 這些值
第二行:2 3 4 5 6
第三行:3 4 5 6 7
第四行:4 5 6 7 8
輸出
大小為 4x5 的矩陣如下所示
a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8
讓我們在 MATLAB 命令視窗中測試矩陣建立,如下所示 -
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >>
引用元素
要引用矩陣 mx 中第 m 行第 n 列的元素,我們編寫以下內容
mx(m, n);
示例
要引用在上節中建立的矩陣 a 中第 2 行第 5 列的元素,我們輸入以下內容。
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> a(2,5) ans = 6 >>
要獲取矩陣中第 n 列的所有元素,您可以使用 A(:,n),其中 n 表示矩陣中的列號。
A(:,n).
示例
現在,讓我們從矩陣 a 的第 4 列的所有元素建立一個列向量 v。這將如下所示
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; v = a(:,4)
輸出
MATLAB 將執行上述語句並返回以下結果。
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> v=a(:,4) v = 4 5 6 7 >>
您還可以選擇第 m 到第 n 列中的元素。為此,我們編寫如下內容。
a(:,m:n)
示例
讓我們透過獲取第二列和第三列的元素建立一個較小的矩陣,如下所示 -
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a(:, 2:3)
輸出
MATLAB 將執行上述語句並返回以下結果 -
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> a(:, 2:3) ans = 2 3 3 4 4 5 5 6 >>
同樣,您可以透過獲取矩陣的一部分來建立子矩陣。
示例
讓我們透過獲取 a 的內部子部分建立一個子矩陣 sab,如下所示 -
3 4 5 4 5 6
在 MATLAB 命令視窗中執行期間,矩陣將如下所示 -
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 >> sa = a(2:3,2:4) sa = 3 4 5 4 5 6 >>
Matlab矩陣 - 環境設定
MATLAB 的官方網站是 https://www.mathworks.com。
您的螢幕上將出現以下頁面 -

要下載 MATLAB,請訪問 https://in.mathworks.com/downloads/,如下所示 -
MATLAB 不是免費下載的,您需要支付許可證副本的費用。稍後您可以下載它。
提供了一個免費試用版本,您需要為您的帳戶建立登入資訊。建立帳戶後,他們允許您下載 MATLAB 以及一個線上版本,試用期為 30 天的許可證。

完成從其網站建立登入資訊後,下載 MATLAB 並安裝到您的系統上。然後,啟動 MATLAB,或者您也可以使用他們在您登入後可用的線上版本。
當您安裝 matlab 或點選 MATLAB 的線上連結時,MATLAB 的 UI 介面如下所示。
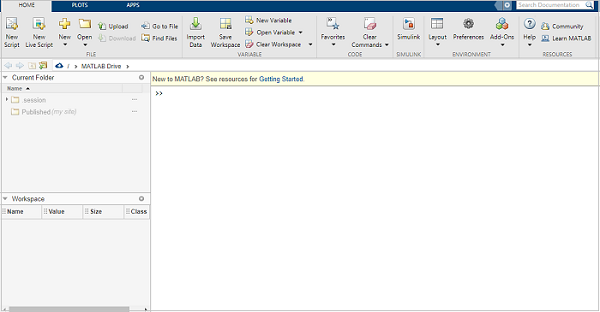
瞭解 MATLAB 環境
MATLAB 開發 IDE 可以從桌面上建立的圖示啟動。MATLAB 中的主要工作視窗稱為桌面。啟動 MATLAB 時,桌面將以其預設佈局顯示。
正如我之前所說,如果您使用的是試用版,可以使用 MATLAB 的線上連結獲取 IDE,如下所示 -
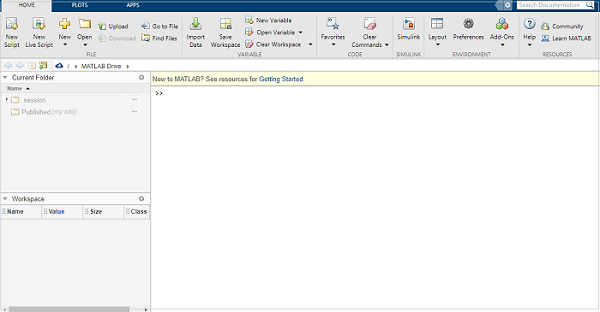
讓我們瞭解 MATLAB IDE。
當前資料夾
此面板允許您訪問專案資料夾和檔案。
命令視窗
這是可以在命令列輸入命令的主要區域。它由命令提示符 (>>) 表示。

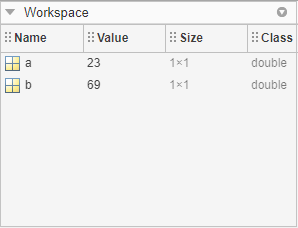
工作區
工作區顯示從檔案建立和/或匯入的所有變數。
Matlab矩陣 - 建立矩陣
在 MATLAB 中,您可以透過輸入每一行中以逗號分隔的元素來建立矩陣。您還可以使用空格分隔的數字和分號來標記每一行的結束來建立矩陣。
單行矩陣
讓我們在 MATLAB 中建立一個簡單的矩陣,它只有一行和三個元素。每個元素都應該有一個空格或逗號。
示例
考慮下面提到的元素來建立矩陣。
m=[2, 4, 6]
輸出
在 MATLAB 中執行時,它將顯示以下內容 -
>>m = [2, 4, 6] m = 2 4 6 >>
當您在 MATLAB 中執行程式碼時,矩陣的結果將在命令視窗中顯示。
多行矩陣
示例
現在讓我們建立一個具有多行的矩陣。為此,我們需要用分號 (;) 分隔每一行,如下所示 -
m = [2 4 6; 3 6 9; 4 8 12]
輸出
這裡2 4 6是第一行,3 6 9是第二行,4 8 12是第三行。矩陣將如下所示 -
m = 2 4 6
3 6 9
4 8 12
現在讓我們在 MATLAB 命令提示符下執行相同的操作,如下所示 -
>> m = [2 4 6; 3 6 9; 4 8 12] m = 2 4 6 3 6 9 4 8 12 >>
3x3 矩陣如上所示在 MATLAB 中顯示。
除了建立包含您選擇的值的矩陣外,您還可以使用內建的 MATLAB 函式 zeros、rand 或 ones 來建立矩陣,如下所示 -
zeros 函式
這將建立一個包含所有零的矩陣,並具有給定的行/列大小。
示例
您可以如下使用 MATLAB zeros 函式 -
m0 = zeros(3,3)
輸出
您將獲得以下輸出 -
>> m0 = zeros(3,3) m0 = 0 0 0 0 0 0 0 0 0 >>
ones 函式
建立的矩陣將以 1 作為值。
示例
您可以如下使用 MATLAB ones 函式 -
m1 = ones(3,3)
輸出
您將獲得以下輸出 -
>> m1 = ones(3,3) m1 = 1 1 1 1 1 1 1 1 1 >>
rand() 函式
rand() 函式允許您為給定的大小建立一個包含隨機元素的矩陣。以下是一個示例。
示例
m1 = rand(3,3)
輸出
現在讓我們在 MATLAB 中執行相同的操作以檢視結果。輸出如下 -
>> m1 = rand(3,3) m1 = 0.8147 0.9134 0.2785 0.9058 0.6324 0.5469 0.1270 0.0975 0.9575 >>
Matlab矩陣 - 矩陣操作
在本章中,我將介紹如何在 MATLAB 環境中執行矩陣以獲取輸出。定義矩陣和其他矩陣運算將在接下來的章節中詳細討論。
要在 MATLAB 中獲得矩陣輸出,將使用 -
- 命令提示符
- 使用 m 檔案
使用命令提示符
您可以直接在命令提示符中執行矩陣。以下是一個示例,其中我們有兩個矩陣a和b。
操作a+b給出矩陣a和b的和。
操作a-b給出矩陣a和b的差。
命令提示符的輸出如下所示 -
>> a = [ 1 2 3 ; 4 5 6; 7 8 9];
>> b = [ 7 5 6 ; 2 0 8; 5 7 1];
>> c = a + b
c =
8 7 9
6 5 14
12 15 10
>> d = a - b
d =
-6 -3 -3
2 5 -2
2 1 8
>>
使用 m 檔案
您還可以使用檔案編寫程式碼,然後在命令提示符下執行它,如下所示 -
單擊“新建指令碼”,如下所示 -
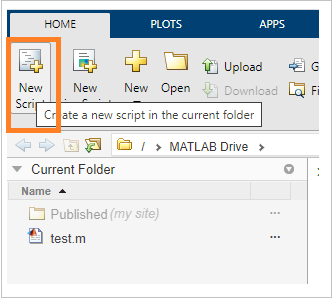
這將開啟一個新的未儲存檔案,如下所示 -

儲存檔案並在其中編寫您的程式碼
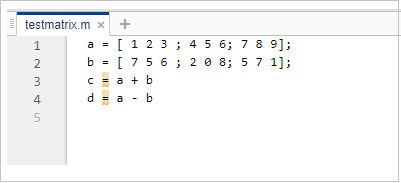
該檔案儲存為 testmatrix.m。
現在,您可以使用執行按鈕或在命令視窗中鍵入檔名。
輸出將在命令視窗中顯示,如下所示 -
>> testmatrix
c =
8 7 9
6 5 14
12 15 10
d =
-6 -3 -3
2 5 -2
2 1 8
>>
Matlab矩陣 - 矩陣乘法
考慮兩個矩陣 A 和 B。如果 A 是一個m x n矩陣,B 是一個n x p矩陣,則可以將它們相乘以生成一個 m x n 矩陣 C。只有當 A 中的列數 n 等於 B 中的行數 n 時,矩陣乘法才可能。
在矩陣乘法中,第一個矩陣中行的元素與第二個矩陣中相應的列相乘。
結果矩陣 C 中的 (i, j) 位置的每個元素都是第一個矩陣的第 i 行的元素與第二個矩陣的第 j 列中相應元素的乘積之和。
MATLAB 中的矩陣乘法是使用 * 運算子執行的。
示例
考慮 MATLAB 中的以下示例
a = [ 1 2 3; 2 3 4; 1 2 5]; b = [ 2 1 3 ; 5 0 -2; 2 3 -1]; prod = a * b
輸出
MATLAB 中的執行將顯示以下結果 -
>> a = [ 1 2 3; 2 3 4; 1 2 5];
b = [ 2 1 3 ; 5 0 -2; 2 3 -1];
prod = a * b
prod =
18 10 -4
27 14 -4
22 16 -6
>>
mtimes 函式
您還可以使用mtimes函式來乘以兩個給定的矩陣。它是 MATLAB 中可用的內建函式。
示例
考慮以下示例 -
a = [ 1 2 3; 2 3 4; 1 2 5]; b = [ 2 1 3 ; 5 0 -2; 2 3 -1]; test= mtimes(a,b)
輸出
在 MATLAB 中執行後,輸出如下 -
>> a = [ 1 2 3; 2 3 4; 1 2 5];
b = [ 2 1 3 ; 5 0 -2; 2 3 -1];
test= mtimes(a,b)
test =
18 10 -4
27 14 -4
22 16 -6
>>
Matlab矩陣 - 矩陣加法
要新增兩個矩陣,兩個運算元矩陣都必須具有相同數量的行和列。
示例
這是一個例子
a = [ 1 2 3 ; 4 5 6; 7 8 9]; b = [ 7 5 6 ; 2 0 8; 5 7 1]; c = a + b
輸出
在 MATLAB 中執行後,結果如下 -
>> a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = a + b
c =
8 7 9
6 5 14
12 15 10
>>
plus() 函式
您還可以使用 plus() 內建函式來新增兩個矩陣,如下所示 -
示例
考慮以下使用 plus() 函式新增兩個矩陣的示例 -
a = [ 1 2 3 ; 4 5 6; 7 8 9]; b = [ 7 5 6 ; 2 0 8; 5 7 1]; c = plus(a,b)
輸出
MATLAB 中的執行結果如下所示:
>> a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = plus(a,b)
c =
8 7 9
6 5 14
12 15 10
>>
Matlab矩陣 - 矩陣減法
要減去兩個矩陣,兩個運算元矩陣必須具有相同數量的行和列。
示例
以下是一個示例:
a = [ 1 2 3 ; 4 5 6; 7 8 9]; b = [ 7 5 6 ; 2 0 8; 5 7 1]; c = a - b
輸出
在 MATLAB 中執行後,結果如下 -
>> a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = a - b
c =
-6 -3 -3
2 5 -2
2 1 8
>>
minus() 函式
您還可以使用內建的 minus() 函式來減去兩個矩陣。
示例
考慮以下使用 minus() 函式減去兩個矩陣的示例:
a = [ 1 2 3 ; 4 5 6; 7 8 9]; b = [ 7 5 6 ; 2 0 8; 5 7 1]; c = minus(a , b)
輸出
您將得到以下結果:
>> a = [ 1 2 3 ; 4 5 6; 7 8 9];
b = [ 7 5 6 ; 2 0 8; 5 7 1];
c = minus(a , b)
c =
-6 -3 -3
2 5 -2
2 1 8
>>
Matlab 矩陣 - 行列式
矩陣的行列式是透過使用 MATLAB 的 det 函式計算的。例如,矩陣 A 的行列式由 det(A) 給出。
示例
考慮以下計算矩陣行列式的示例:
a = [ 1 2 3; 2 3 4; 1 2 5]; test = det(a)
輸出
在 MATLAB 中執行程式碼如下:
>> a = [ 1 2 3; 2 3 4; 1 2 5]; test = det(a) test = -2 >>
Matlab矩陣 - 逆矩陣
矩陣 A 的逆表示為 A−1,滿足以下關係:
AA−1 = A−1A = 1
矩陣的逆並不總是存在。如果矩陣的行列式為零,則逆不存在,矩陣是奇異的。
MATLAB 中矩陣的逆是使用 inv 函式計算的。矩陣 A 的逆由 inv(A) 給出。
示例
以下是如何計算給定矩陣的逆的示例:
a = [ 1 2 3; 2 3 4; 1 2 5]; test = inv(a)
輸出
MATLAB 中的執行結果如下:
>> a = [ 1 2 3; 2 3 4; 1 2 5];
test = inv(a)
test =
-3.5000 2.0000 0.5000
3.0000 -1.0000 -1.0000
-0.5000 0 0.5000
>>
Matlab矩陣 - 跡
跡有助於計算給定矩陣中對角元素的和。
示例
考慮給定的 3x3 矩陣。讓我們找出對角元素的和,如下所示:
a = [ 1 2 3; 2 3 4; 1 2 5]; test = trace(a)
輸出
MATLAB 中的執行結果如下:
>> a = [ 1 2 3; 2 3 4; 1 2 5] test = trace(a) a = 1 2 3 2 3 4 1 2 5 test = 9 >>
Matlab矩陣 - 秩
矩陣的秩是矩陣中線性無關列的數量。rank() 函式有助於返回給定矩陣的秩。
示例
考慮以下使用 rank() 函式計算矩陣秩的示例:
a = [ 1 2 3; 2 3 4; 1 2 5] test = rank(a)
輸出
MATLAB 中執行程式碼後的輸出如下:
>> a = [ 1 2 3; 2 3 4; 1 2 5] test = rank(a) a = 1 2 3 2 3 4 1 2 5 test = 3 >>
Matlab矩陣 - 轉置
轉置操作交換矩陣中的行和列。它由單引號 (') 表示。
示例
考慮以下示例 -
a = [ 10 12 23 ; 14 8 6; 27 8 9] b = a'
輸出
MATLAB 中的執行結果如下:
>> a = [ 10 12 23 ; 14 8 6; 27 8 9] b = a' a = 10 12 23 14 8 6 27 8 9 b = 10 14 27 12 8 8 23 6 9 >>
transpose() 函式
您還可以使用 transpose() 函式來獲取矩陣的轉置。
示例
考慮以下使用 transpose() 函式的示例:
a = [ 10 12 23 ; 14 8 6; 27 8 9] b = transpose(a)
輸出
您將獲得以下輸出 -
>> a = [ 10 12 23 ; 14 8 6; 27 8 9] b = transpose(a) a = 10 12 23 14 8 6 27 8 9 b = 10 14 27 12 8 8 23 6 9 >>
Matlab 矩陣 - 刪除行和列
您可以透過將空方括號 [] 分配給該行或列來刪除矩陣的整行或整列。基本上,[] 表示空陣列。
示例
例如,讓我們刪除 a 的第四行,如下所示:
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a( 4 , : ) = []
輸出
以下是上述程式碼在 MATLAB 中的執行結果
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a( 4 , : ) = [] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 >>
第四行已刪除。它只顯示三行。
示例
接下來,讓我們刪除 a 的第五列,如下所示:
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a(: , 5)=[]
輸出
讓我們看看上述程式碼在 MATLAB 中的執行結果:
>> a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8] a(: , 5)=[] a = 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 a = 1 2 3 4 2 3 4 5 3 4 5 6 4 5 6 7 >>