機器學習中K-Medoids聚類及其解題示例

---

簡介

K-Medoids 是一種使用分割槽聚類方法的無監督聚類演算法。它是 K-Means 聚類演算法的改進版本，特別用於處理異常值資料。它需要無標籤資料才能工作。

在本文中，讓我們透過一個例子來了解 k-Medoids 演算法。

K-Medoids 演算法

在 K-Medoids 演算法中，每個資料點都被稱為類中心點(medoid)。類中心點充當聚類中心。類中心點是指其與同一聚類中所有其他點的距離之和最小的點。對於距離，可以使用任何合適的度量，如歐幾里得距離或曼哈頓距離。

應用演算法後，完整的資料將被分成 K 個聚類。

K-Medoids 有三種類型 - PAM、CLARA 和 CLARANS。PAM 是最流行的方法。它有一個缺點，即需要大量時間。

K-Medoid 的應用方式如下：

• 一個點只能屬於一個聚類。

• 每個聚類至少包含一個點。

讓我們透過一個例子看看 K-Medoids 的工作流程。

工作原理

最初，我們有 K 表示聚類的數量，D 表示我們的無標籤資料。

• 首先，我們從資料集中選擇 K 個點並將它們分配給 K 個聚類。這 K 個點充當初始類中心點。每個物件都被納入一個聚類。

• 接下來，使用歐幾里得距離、曼哈頓距離等距離度量計算初始類中心點（點）與其他點（非類中心點）之間的距離。

• 非類中心點被分配到其到類中心點距離最小的特定聚類。

• 現在計算總成本，即聚類內其他點到類中心點的距離之和。

• 接下來，選擇一個隨機的新非類中心點 s 並將其與初始類中心點 r 交換，然後重新計算成本。

• 如果成本 < costr，則交換成為永久性。

• 最後，重複步驟 2 到 6，直到成本不再發生變化。

示例

讓我們考慮以下資料集。我們將取 k=2，並使用以下距離公式：

$$\mathrm{D=\mid x_{2}-x_{1}\mid+\mid y_{2}-y_{1}\mid}$$

序號	x	y
1	9	6
2	10	4
3	4	4
4	5	8
5	3	8
6	2	5
7	8	5
8	4	6
9	8	4
10	9	3

將資料繪製到圖表上後，其外觀類似於下圖。

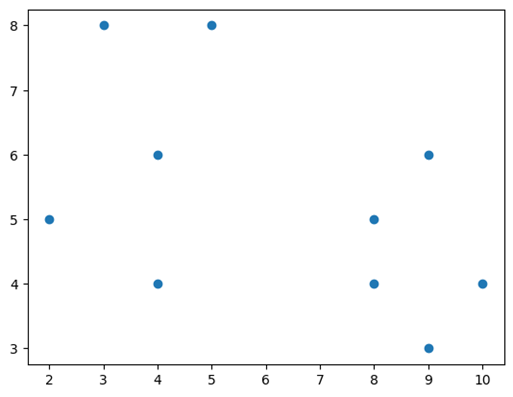
對於 k = 2，讓我們取兩個隨機點 P1(8,4) 和 P2(4,6)，並計算它們到其他點的距離。

序號	x	y	P1 (8,4) 的距離	P2 (4,6) 的距離
1	9	6	3	5
2	10	4	2	8
3	4	4	4	2
4	5	8	7	3
5	3	8	9	3
6	2	5	7	3
7	8	5	1	5
8	4	6	-	-
9	8	4	-	-
10	9	3	2	8

1,2,7,10 - 分配給 P1(8,4)

3,4,5,6 - 分配給 P2(4,6)

涉及的總成本 C1 = (3+2+1+2) +(2+3+3+3) = 19

現在讓我們隨機選擇其他兩個點作為類中心點 P1(8,5) 和 P2(4,6)，並計算距離。

序號	x	y	P1(8,5) 的距離	P2(4,6) 的距離
1	9	6	2	5
2	10	4	3	8
3	4	4	5	2
4	5	8	6	3
5	3	8	6	3
6	2	5	6	3
7	8	5	-	-
8	4	6	-	-
9	8	4	1	-
10	9	3	3	8

$$\mathrm{新的成本 C_{2}=[2+3+1+3]+[2+3+3+3]=20}$$

$$\mathrm{交換涉及的總成本 C=C_{2}-C_{1}=20-19=1}$$

由於交換涉及的總成本 C 大於 0，因此我們不恢復交換。

點 P1(8,4) 和 P2(4,6) 被認為是最終的類中心點，並且僅使用這些點形成了 2 個聚類。

程式碼實現

import numpy as np
from sklearn_extra.cluster import KMedoids

data = {'x' : [9,10,4,5,3,2,8,4,8,9],
'y' : [6,4,4,8,8,5,5,6,4,3]}

x = [[i,j] for i,j in zip(data['x'],data['y'])]

data_x = np.asarray(x)
model_km = KMedoids(n_clusters=2)
km = model_km.fit(data_x)
print("Labels :",km.labels_)
print("Cluster centers  :",km.cluster_centers_)

輸出

Labels : [1 1 0 0 0 0 1 0 1 1]
Cluster centers  : [[4. 6.]
 [8. 4.]]

結論

K-Medoids 是對 M-Means 演算法的改進方法。它是非監督的，需要無標籤資料。K-Mediods 是一種基於距離的方法，它依賴於聚類之間的距離和聚類內的距離，其中類中心點充當聚類中心，並被用作計算距離的參考點。它非常有用，因為它可以非常有效地處理異常值。