Python中的逆伽馬分佈

---

簡介

逆伽馬分佈是一種連續機率分佈，在貝葉斯統計、經濟學和物理學等許多學科中出現。它作為正態分佈中精度引數的共軛先驗，並且常用於表示具有正偏度的變數。本文涵蓋了逆伽馬分佈、其描述、Python中的語法以及帶有工作程式碼的示例，以演示如何使用它。

逆伽馬分佈

定義

逆伽馬分佈是在正實數線上定義的機率分佈。它由兩個引數描述：形狀（alpha）和尺度（beta）。逆伽馬分佈的機率密度函式（PDF）由以下公式給出：

f(x|alpha, beta) = (betaalpha / math.gamma(alpha)) * x(-alpha-1) * exp(-beta / x)

其中 x > 0，alpha > 0，beta > 0，並且 math.gamma 表示伽馬函式。

語法

可以使用 Python 中的 scipy.stats 模組來處理逆伽馬分佈，該模組提供了大量機率分佈。以下是構建逆伽馬分佈物件的語法：

from scipy.stats import invgamma
# Creating an Inverse Gamma distribution object
inverse_gamma_dist = invgamma(alpha, scale=beta)

您可以複製上述程式碼片段並將 alpha 和 beta 更改為逆伽馬分佈的形狀和尺度引數的所需值。請注意，使用逆伽馬分佈需要在您的 Python 環境中安裝 scipy.stats 模組。

語法解釋

• ‘from scipy.stats import invgamma’：此行匯入 scipy.stats 模組的 invgamma 類。

• ‘inverse_gamma_dist = invgamma(alpha, scale=beta)’：在此行中，alpha 用作形狀引數，beta 用作尺度引數，以生成逆伽馬分佈的例項。

演算法

• 步驟 1 - 匯入所需的庫

• 步驟 2 - 定義形狀和尺度引數

• 步驟 3 - 建立一個逆伽馬分佈物件

• 步驟 4 - 從逆伽馬分佈生成隨機數

• 步驟 5 - 繪製生成的數字的機率密度函式（PDF）和直方圖

方法

• 方法 1 - 生成隨機數

• 方法 2 - 機率密度函式（PDF）

方法 1：生成隨機數

在此方法中，我們使用逆伽馬分佈物件的 rvs 方法從逆伽馬分佈生成隨機數。我們可以透過選擇 size 引數來控制生成的隨機數的數量。

示例

import numpy as np
from scipy.stats import invgamma

# Define the shape and scale parameters
alpha = 3
beta = 2

# Create an Inverse Gamma distribution object
inverse_gamma_dist = invgamma(alpha, scale=beta)

# Generate random numbers from the Inverse Gamma distribution
random_numbers = inverse_gamma_dist.rvs(size=1000)

print(random_numbers)

輸出

[0.50492148 0.99333748 1.75490027 ... 0.65061424 0.70721182 0.78544613]

方法 1 的主要目標是使用逆伽馬分佈生成隨機數。逆伽馬分佈物件的 rvs 方法可用於快速生成所需數量的隨機樣本。在此方法中，我們首先指定逆伽馬分佈的形狀 (alpha) 和尺度 (beta) 引數。接下來，我們使用 scipy.stats 模組中的 invgamma 類生成逆伽馬分佈的例項。透過在分佈物件上使用 rvs 方法並提供所需的 size，使用逆伽馬分佈生成一組隨機數。使用此方法，可以生成隨機數來模擬資料或為各種目的執行蒙特卡羅模擬。

請注意，由於生成的隨機數是隨機生成的，因此每次執行程式碼時它們都會有所不同。

方法 2：機率密度函式（PDF）

在此方法中，我們使用逆伽馬分佈物件的 pdf 方法來視覺化分佈的機率密度函式（PDF）。這使我們能夠看到分佈的形狀並理解其屬性。

示例

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import invgamma

# Define the shape and scale parameters
alpha = 2.5
beta = 1.2

# Create an Inverse Gamma distribution object
inverse_gamma_dist = invgamma(alpha, scale=beta)

# Generate an array of x values
x = np.linspace(0.001, 10, 100)

# Calculate the PDF values for the x values
pdf_values = inverse_gamma_dist.pdf(x)

# Plot the PDF of the Inverse Gamma distribution
plt.plot(x, pdf_values, 'r-', label='PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.title('PDF of Inverse Gamma Distribution')
plt.legend()
plt.show()

輸出

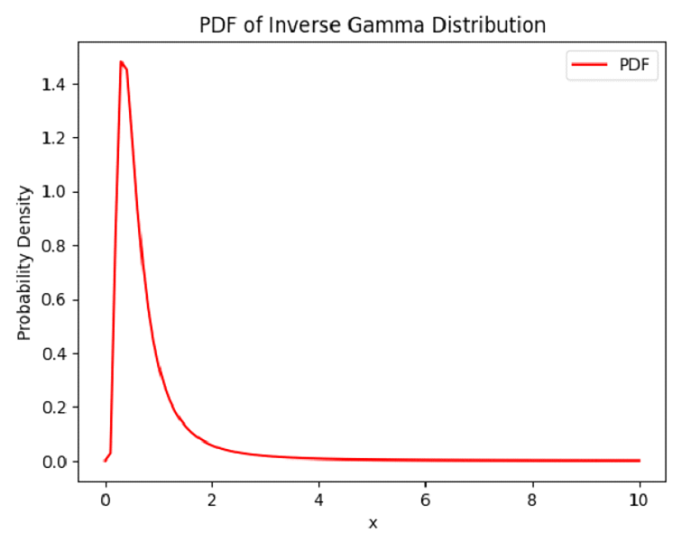
在此方法中，我們首先使用 np.linspace 函式生成一個從 0.001 到 10 之間 100 個均勻間隔的值的陣列。這些 x 值表示我們想要評估 PDF 的範圍。然後，使用逆伽馬分佈物件的 pdf 方法計算生成 x 值的機率密度函式（PDF）值。結果，我們得到每個 x 值的 PDF 值陣列。

最後，我們使用 matplotlib.pyplot 模組的 plt.plot 方法繪製逆伽馬分佈的 PDF。生成的繪圖在 x 軸上顯示 x 值，在 y 軸上顯示 PDF 值，從而顯示分佈的形狀。透過視覺化 PDF，我們可以看到重要的細節，如分佈的位置、散佈和偏度。使用此方法可以更好地理解逆伽馬分佈及其行為。

請注意，當您執行程式碼時，生成的繪圖將顯示在單獨的視窗中。

結論

逆伽馬分佈是一種靈活的機率分佈，應用於許多不同的領域。在本文中，我們討論了其描述、Python 語法以及帶有工作程式碼的示例，以演示如何使用它。透過掌握基礎知識並利用 scipy.stats 模組，您可以使用逆伽馬分佈在 Python 中對資料建模和分析。逆伽馬分佈有許多應用，包括貝葉斯分析、金融和物理學。它提供了一種通用且有效的方法來對具有正偏度的變數建模。透過利用本文中提供的概念和示例，您可以自信地將逆伽馬分佈新增到您的 Python 資料分析專案中。

無論您需要生成隨機數還是檢查分佈的特性，Python 和 scipy.stats 模組都提供了處理逆伽馬分佈所需的所有工具。