資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會研究
服裝研究
法律研究如何在計算理論 (TOC) 中使用圖靈機識別語言？
圖靈機 (TM) 可以正式描述為七元組：
(Q,X, ∑, δ,q0,B,F)
其中：
Q 是有限狀態集。
X 是帶字母表。
∑ 是輸入字母表。
δ 是轉移函式：𝛿:QxX->QxXx{左移，右移}。
q0 是初始狀態。
B 是空白符號。
F 是最終狀態。
當且僅當圖靈機 T 從初始位置開始，x 寫在磁帶上，並且 T 停留在最終狀態時，圖靈機 T 識別字符串 x（在 ∑ 上）。
T 停留在最終狀態。
如果 x 被 T 識別，當且僅當 x 屬於 A 時，則稱 T 識別語言 A。
請注意，在執行 TM 時，您還可以讀取/寫入磁帶上的其他符號，而不必僅限於字母表 A 中的符號。
如果圖靈機 T 沒有停留在非最終狀態，則它不識別字符串 x。
有些 TM 對於某個輸入根本不會停止，而是一直執行。
瞬時描述
要描述給定時間的 TM，我們需要了解以下三點：
磁帶上有什麼？
磁頭在哪裡？
控制處於什麼狀態？
我們將用以下方式表示此資訊：
狀態 i − B a a b a b B
這裡，B 符號表示空單元格（無限重複到左邊和右邊），磁頭的位置以紅色顯示。
示例
對於 ∑ = {a, b}，設計一個接受由正則表示式 a* 表示的語言的圖靈機。
步驟 1 - 從輸入的左端開始，我們讀取每個符號並檢查它是否是 a。
步驟 2 - 如果是，我們繼續向右移動。
步驟 3 - 如果我們在遇到除 a 之外的任何符號之前到達空白符號，我們終止並接受該字串。
步驟 4 - 如果輸入在任何地方包含 b（字串不在 L(a*) 中），我們會在非最終狀態下停止。
為了跟蹤計算，兩個狀態 0（初始）和 1（最終）就足夠了。作為轉移函式，我們可以使用：
T(0, a) = (0, a, R),
T(0,B ) = (1,B , R)
或者我們可以畫一個圖：
更新於：2021年6月16日
969 次瀏覽
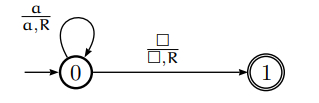
廣告