資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究在計算理論中解釋多磁帶圖靈機？
具有多個磁帶的圖靈機（TM）稱為多磁帶圖靈機。
每個磁帶都有自己的讀/寫磁頭。
對於 N 磁帶圖靈機
M={( Q,X, ∑,δ,q0,B,F)}
我們將多磁帶圖靈機定義為具有 k 個磁帶和 k 個磁頭獨立移動的機器（多軌跡圖靈機的推廣）。
δ=QxXN ->Q x XN x {L,R}N
每個 TM 都有自己的讀寫磁頭，但狀態對所有磁頭都是共有的。多磁帶 TM 如下所示：
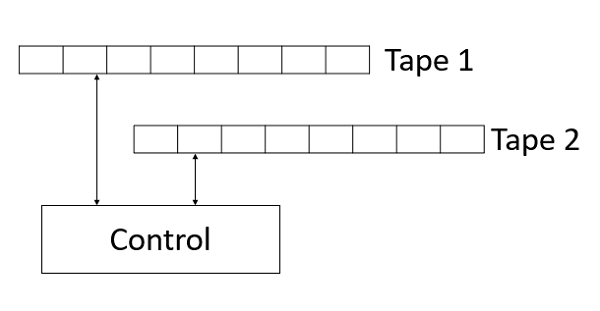
在每個步驟（轉換）中，TM 讀取所有磁頭掃描的符號，根據這些符號和當前狀態，每個磁頭寫入、向右或向左移動，以及控制單元進入新狀態。
磁頭的動作彼此獨立。
示例
將兩個數字（每個數字都表示為一個一元字串）相乘以得到第三個數字，這對於簡單的圖靈機來說很難做到，但對於三磁帶機器來說卻相當簡單。
計算開始前的磁帶 計算開始前第二次加法的磁帶
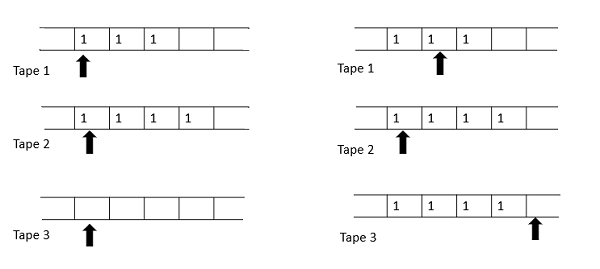
首先檢查這兩個數字是否為零：
(0,(B,B ,B ),(B,B ,B ),(S, S, S), Halt) 兩者都為零
(0,(B, 1, B),(B, 1,B ),(S, S, S), Halt) 第一個為零
(0,(1,B ,B ),(1,B ,B ),(S, S, S), Halt) 第二個為零
(0,(1, 1, B),(1, 1B, ),(S, S, S), 1) 兩者都不為零
將第二個磁帶上的數字加到第三個磁帶上：
(1,(1, 1,B ),(1, 1, 1),(S, R, R), 1) 複製
(1,(1,B ,B ),(1,B ,B ),(S, L, S), 2) 完成複製
將第二個磁帶的磁頭移動到數字的左端；將第一個數字的磁頭向右移動一個單元格：
(2,(1, 1,B ),(1, 1,B ),(S, L, S), 2) 移動到左端
(2,(1,B ,B ),(1,B ,B ),(R, R, S), 3) 兩種型別都向右移動一個單元格
檢查第一個磁帶磁頭以檢視是否已執行所有加法：
(3,(B, 1,B ),(B, 1,B ),(S, S, L), Halt) 完成
(3,(1, 1,B ),(1, 1,B ),(S, S, S), 1) 執行另一個加法
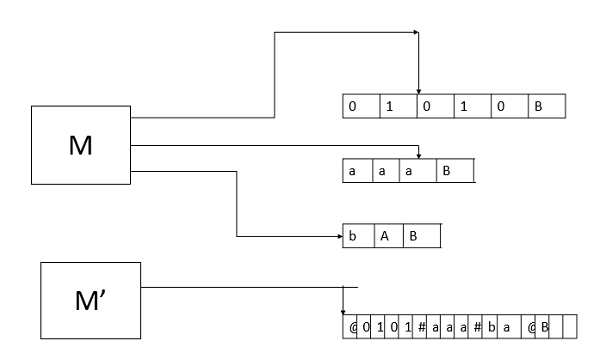
每個多磁帶 TM 都有一個等效的單磁帶 TM。
如果 M 有 k 個磁帶，則 M0 透過在其單個磁帶上儲存相同的資訊來模擬 k 個磁帶的效果。
使用新的符號 # 作為分隔符來分隔不同磁帶的內容（標記相關磁帶部分的左/右端）。
M0 還必須跟蹤每個磁帶上磁頭的位置。
在磁帶符號上寫一個帶點的符號以標記該磁帶上磁頭所在的位置。帶點符號只是新增到磁帶字母表中的新符號。
如果一個 T 的磁帶磁頭的移動導致 M0 的磁頭撞到 # 或 #，則必須移動磁帶的該側以騰出空間用於新的磁帶單元格。
4K+ 次檢視
