資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究如何測量中等電阻？(電阻測量方法)
大約 **1Ω** 到 **100 kΩ** 之間的電阻被歸類為 **中等電阻**。大多數電氣裝置的電阻都是中等電阻的例子。
中等電阻的測量
為了測量中等電阻，使用以下方法：
電流表-電壓表法
替代法
惠斯通電橋
凱里-福斯特滑線電橋法。
電流表-電壓表法
在這種方法中，同時測量未知電阻 (Rx) 中的電流和跨越它的電壓降。讀數分別由電流表和電壓表獲得。電流表和電壓表可以有兩種連線方式進行測量，如下所示：
**情況 1** – 當電壓表直接連線到電阻兩端時，電流表測量流過未知電阻 (Rx) 和電壓表的電流。
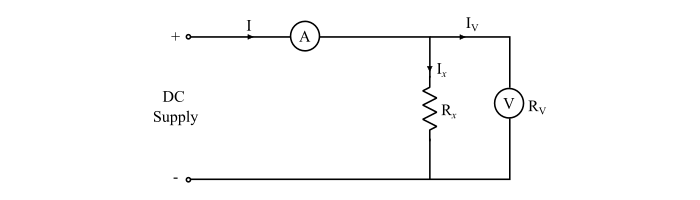
流過電流表的電流 = 流過 (𝑅x) 的電流 + 流過電壓表的電流
$$\mathrm{I=I_{R_{x}}+I_{V}}$$
$$\mathrm{\Rightarrow\:I_{R_{x}}=I-I_{V}}$$
因此，未知電阻的值為：
$$\mathrm{R_{X}=\frac{V}{I_{X}}=\frac{V}{I-I_{V}}=\frac{V}{I-(V/R_{V})}\:\:\:...(1)}$$
**情況 2** – 當電流表連線使得它只測量流過未知電阻 (Rx) 的電流時，電壓表測量跨越電流表和 Rx 的電壓降。
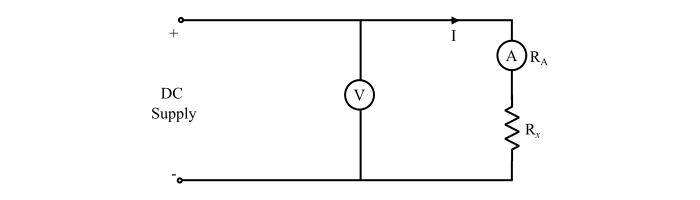
因此，
$$\mathrm{V=IR_{A}+IR_{X}=I(R_{A}+R_{X})}$$
$$\mathrm{\Rightarrow\:R_{X}=\frac{V}{I}-R_{A}\:\:\:\:...(2)}$$
替代法
**步驟 1** – 在此方法中，首先將未知電阻 (Rx) 放入電路中並記錄電流值。
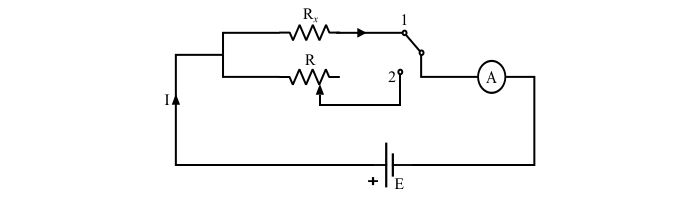
**步驟 2** – 然後移除電阻 Rx，並用已知的可變電阻 R 替代 它，並改變 R 的值，使電流值在兩種情況下都相同。這個 R 的值等於未知電阻的值。
惠斯通電橋
惠斯通電橋方法是測量電阻最準確的方法。
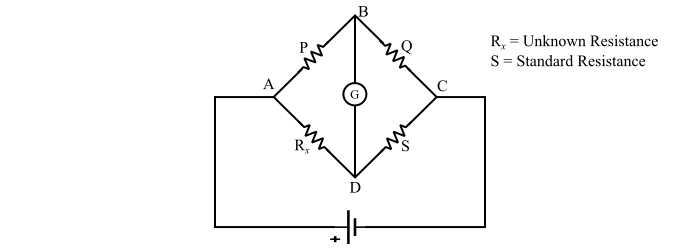
該電橋由四個電阻臂、一個電動勢源和一個檢流計（零檢測器）組成。流過檢流計的電流取決於 B 和 D 兩點之間的電位差。當檢流計上的電位差為零時，據說電橋處於平衡狀態，因此沒有電流流過檢流計。
對於平衡的惠斯通電橋，
$$\mathrm{PS=QR_{x}}$$
$$\mathrm{\Rightarrow\:R_{x}=\frac{PS}{Q}\:\:\:...(3)}$$
凱里-福斯特滑線電橋法
該電橋的電路是惠斯通電橋的擴充套件形式，專門用於比較兩個幾乎相等的電阻。
電路由四個電阻臂組成，其中 R1 和 R2 是比率臂，R3 是標準電阻，Rx 是未知電阻。一個長度為 l 且橫截面積均勻的滑線（m-n）連線在 R3 和 Rx 之間。滑線每單位長度的電阻為 r Ω。
調整電阻 R1 和 R2，使比率 $\mathrm{(\frac{R_{1}}{R_{2}})}$ 約等於比率 $\mathrm{(\frac{R_{x}}{R_{3}})}$。透過調整滑線上的滑動觸點來獲得此平衡。然後，對於第一次平衡，設l1 是滑動觸點距滑線 m 點的距離。因此，
$$\mathrm{\frac{R_{1}}{R_{2}}=\frac{R_{x}+l_{1}r}{R_{3}+(l-l_{1})r}\:\:\:...(4)}$$
對於第二次平衡，設l2 是距滑線 m 點的距離，並且交換電阻 Rx 和 R3，則
$$\mathrm{\frac{R_{1}}{R_{2}}=\frac{R_{3}+l_{2}r}{R_{x}+(l-l_{2})r}\:\:\:...(5)}$$
由式 (4) 和 (5) 可得，
$$\mathrm{\frac{R_{x}+l_{1}r}{R_{3}+(l-l_{1})r}=\frac{R_{3}+l_{2}r}{R_{x}+(l-l_{2})r}}$$
因此，差值 (R3 – Rx) 由兩個平衡點之間的滑線電阻獲得。
現在，r 的值，即滑線的每單位長度電阻，是透過將已知的高電阻與 R3 並聯獲得的，這將有效值降低到 R3'，因此再次重複上述過程以獲得新的平衡點𝑙1'和𝑙2'，使得，
$$\mathrm{R_{3}^{'}-R_{x}^{'}=r(l_{1}^{'}-l_{2}^{'})\:\:\:\:...(7)}$$
用式 (7) 除式 (6)，得到：
$$\mathrm{\frac{R_{3}-R_{x}}{R_{3}^{'}-R_{x}^{'}}=\frac{r(l_{1}-l_{2})}{r(l_{1}^{'}-l_{2}^{'})}}$$
$$\mathrm{\Rightarrow\:R_{x}=\frac{R_{3}(l_{1}^{'}-l_{2}^{'})-R_{3}^{'}(l_{1}-l_{2})}{(l_{1}^{'}-l_{2}^{'}-l_{1}+l_{2})}\:\:\:\:....(8)}$$
6K+ 次瀏覽
